题目内容
16.如图,梯形ABCD中,AD∥BC,∠B=90°,AD=20cm,AB=8cm,BC=26cm,动点P从点A开始,沿AD边,以2cm/秒的速度向点D运动;动点Q从点C开始,沿CB边,以3cm/秒的速度向B点运动.已知P、Q两点分别从A、C同时出发,当其中一点到达端点时,另一点也随之停止运动.假设运动时间为t秒,问:(1)是否存在某一时刻t,使四边形PQCD是平行四边形?存在,求出t值;不存在请说明理由.
(2)是否存在某一时刻t,使四边形PQCD是直角梯形?存在,求出t值;不存在请说明理由.
(3)在某个时刻,四边形PQCD可能是菱形吗?为什么?
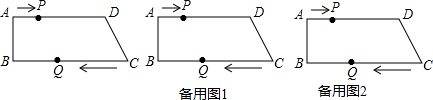
分析 (1)存在,根据对边平行且相等的四边形是平行四边形列出方程,解方程即可;
(2)存在,当APQB为矩形时,四边形PDQC为直角梯形,即AP=BQ;
(3)四边形PQCD不可能是菱形,根据邻边相等的平行四边形是菱形进行计算,比较邻边的长度得到答案.
解答 解:(1)存在;
如图1,当PD=CQ时,四边形PQCD为平行四边形,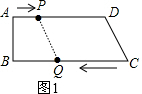
即20-2t=3t,
解得,t=4,
故当t=4时,四边形PQCD为平行四边形;
(2)存在;
如图2,当AP=BQ时,四边形PQCD为直角梯形,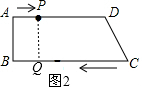
即2t=26-3t
解得:t=5.2,
故当t=5.2时,四边形PQCD为直角梯形;
(3)四边形PQCD不可能是菱形,
如图3,作DE⊥BC于E,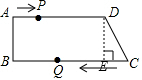
则四边形ABED为矩形,
∴DE=AB=8,EC=2,
∴CD=$\sqrt{D{E}^{2}+C{E}^{2}}$=2$\sqrt{17}$,
若四边形PQCD是菱形,则四边形PQCD是平行四边形,
根据(1)得:t=4s,
∴PD=20-8=12(cm),
∴PD≠CD,
∴四边形PQCD不可能是菱形.
点评 本题考查的是直角梯形和矩形的性质以及平行四边形、菱形的判定,掌握对边平行且相等的四边形是平行四边形、邻边相等的平行四边形是菱形是就的关键.

练习册系列答案
相关题目
6.下列数值中,是不等式x≥-2的解的是( )
| A. | -1 | B. | -3 | C. | -5 | D. | -9 |
11.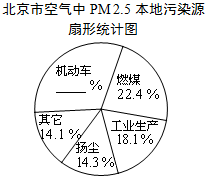 据报道,历经一年半的调查研究,北京PM 2.5源解析已经通过专家论证.各种调查显示,机动车成为PM 2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天至少就要向大气里排放0.035千克污染物.如图是相关的统计图表:
据报道,历经一年半的调查研究,北京PM 2.5源解析已经通过专家论证.各种调查显示,机动车成为PM 2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天至少就要向大气里排放0.035千克污染物.如图是相关的统计图表:
2014年北京市全年空气质量等级天数统计表
(1)请根据所给信息补全扇形统计图;
(2)请你根据“2014年北京市全年空气质量等级天数统计表”计算该年度重度污染和严重污染出现的频率共是多少?(精确到0.01)
(3)小明是社区环保志愿者,他和同学们调查了本社区的100辆机动车,了解到其中每天出行超过20千米的有40辆.已知北京市2014年机动车保有量已突破520万辆,请你通过计算,估计2014年北京市一天中出行超过20千米的机动车至少要向大气里排放多少千克污染物?
 据报道,历经一年半的调查研究,北京PM 2.5源解析已经通过专家论证.各种调查显示,机动车成为PM 2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天至少就要向大气里排放0.035千克污染物.如图是相关的统计图表:
据报道,历经一年半的调查研究,北京PM 2.5源解析已经通过专家论证.各种调查显示,机动车成为PM 2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天至少就要向大气里排放0.035千克污染物.如图是相关的统计图表:2014年北京市全年空气质量等级天数统计表
| 空气质量等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 天数(天) | 41 | 135 | 84 | 47 | 45 | 13 |
(2)请你根据“2014年北京市全年空气质量等级天数统计表”计算该年度重度污染和严重污染出现的频率共是多少?(精确到0.01)
(3)小明是社区环保志愿者,他和同学们调查了本社区的100辆机动车,了解到其中每天出行超过20千米的有40辆.已知北京市2014年机动车保有量已突破520万辆,请你通过计算,估计2014年北京市一天中出行超过20千米的机动车至少要向大气里排放多少千克污染物?
 如图,已知在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,若∠EAF=60°,CE=3cm,FC=1cm,求AB,BC的长及ABCD面积.
如图,已知在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,若∠EAF=60°,CE=3cm,FC=1cm,求AB,BC的长及ABCD面积.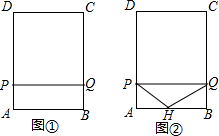 如图①,在矩形ABCD中,AB=9.AD=12.点P从点A出发以每秒3个单位长度的速度沿A-D-C-B-A运动一周到点A停止.当点P不与矩形ABCD的顶点重合时,过点P作直线PQ⊥AP,与矩形的边的另一交点为Q.设点P的运动时间为t(秒).
如图①,在矩形ABCD中,AB=9.AD=12.点P从点A出发以每秒3个单位长度的速度沿A-D-C-B-A运动一周到点A停止.当点P不与矩形ABCD的顶点重合时,过点P作直线PQ⊥AP,与矩形的边的另一交点为Q.设点P的运动时间为t(秒).