题目内容
14.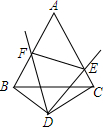 已知△ABC是边长为2的等边三角形,△DBC是顶角为120°的等腰三角形,以点D为顶点作一个60°角,角的两边分别交AB,AC于点E,F,连接EF,则△AEF的周长=4.
已知△ABC是边长为2的等边三角形,△DBC是顶角为120°的等腰三角形,以点D为顶点作一个60°角,角的两边分别交AB,AC于点E,F,连接EF,则△AEF的周长=4.
分析 延长AB到N,使BN=CF,连接DN,求出∠FCD=∠EBD=∠NBD=90°,根据SAS证△NBD≌△FCD,推出DN=DF,∠NDB=∠FDC,求出∠EDF=∠EDN,根据SAS证△EDF≌△EDN,推出EF=EN,即可得到BE+CF=EF,易得△AEF的周长等于AB+AC.
解答 解:如图,延长AB到N,使BN=CF,连接DN,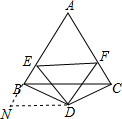 ∵△ABC是等边三角形,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵BD=CD,∠BDC=120°,
∴∠DBC=∠DCB=30°,
∴∠ACD=∠ABD=30°+60°=90°=∠NBD,
∵在△NBD和△FCD中,
$\left\{\begin{array}{l}{BD=DC}\\{∠NBD=∠FCD=90°}\\{BN=CF}\end{array}\right.$,
∴△NBD≌△FCD(SAS),
∴DN=DF,∠NDB=∠FDC,
∵∠BDC=120°,∠EDF=60°,
∴∠EDB+∠FDC=60°,
∴∠EDB+∠BDN=60°,
即∠EDF=∠EDN,
在△EDN和△EDF中,
$\left\{\begin{array}{l}{DE=DE}\\{∠EDF=∠EDN}\\{DN=DF}\end{array}\right.$,
∴△EDN≌△EDF(SAS),
∴EF=EN=BE+BN=BE+CF,
即BE+CF=EF.
∵△ABC是边长为2的等边三角形,
∴AB=AC=2,
∵BE+CF=EF,
∴△AEF的周长为:AE+EF+AF=AE+EB+FC+AF=AB+AC=4.
故答案为:4.
点评 本题考查了等边三角形性质和判定,等腰三角形的性质,三角形的内角和定理,全等三角形的性质和判定的综合运用.注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
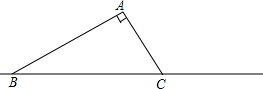 已知,如图,在△ABC中,AC=3厘米,BC=6厘米,∠C=60°,求:
已知,如图,在△ABC中,AC=3厘米,BC=6厘米,∠C=60°,求: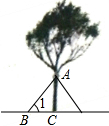 在台风来临之前,有关部门用钢管加固树木(如图).已知固定点A离地面的高度AC为3m,钢管脚的支撑点B离树干底部C点的距离为2m.求钢管与地面所成角∠1的大小(精确到1″).
在台风来临之前,有关部门用钢管加固树木(如图).已知固定点A离地面的高度AC为3m,钢管脚的支撑点B离树干底部C点的距离为2m.求钢管与地面所成角∠1的大小(精确到1″).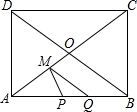 如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=8cm,BC=6cm,定长为2cm的动线段PQ在边AB上,端点P从点A开始沿边AB以1cm/s的速度向点B运动,当端点Q到达点B时运动停止,过点Q作QM∥BD交AC于点M(当点Q与点B重合时,QM与BO重合),连接PM.设线段PQ的运动时间为t(s)(t≥0).
如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=8cm,BC=6cm,定长为2cm的动线段PQ在边AB上,端点P从点A开始沿边AB以1cm/s的速度向点B运动,当端点Q到达点B时运动停止,过点Q作QM∥BD交AC于点M(当点Q与点B重合时,QM与BO重合),连接PM.设线段PQ的运动时间为t(s)(t≥0).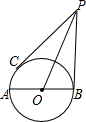 如图,已知点C在以AB为直径的⊙O上,过点B、C作⊙O的切线,且交于点P,联结AC,若OP=$\frac{9}{2}$AC.求$\frac{PB}{AC}$的值.
如图,已知点C在以AB为直径的⊙O上,过点B、C作⊙O的切线,且交于点P,联结AC,若OP=$\frac{9}{2}$AC.求$\frac{PB}{AC}$的值. 在4×4的方格中有五个同样大小的正方形如图摆放,移动其中一个正方形到空白方格中,与其余四个正方形组成的新图形是一个轴对称图形,这样的移法共有( )种.
在4×4的方格中有五个同样大小的正方形如图摆放,移动其中一个正方形到空白方格中,与其余四个正方形组成的新图形是一个轴对称图形,这样的移法共有( )种.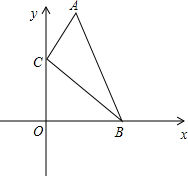 如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上.
如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上.