题目内容
16.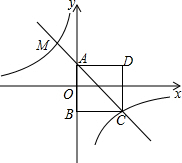 如图,四边形ABCD为正方形,点A的坐标为(0,1),点B的坐标为(0,-2),反比例函数y=$\frac{k}{x}$的图象经过点C,一次函数y=ax+b的图象经过A、C两点.
如图,四边形ABCD为正方形,点A的坐标为(0,1),点B的坐标为(0,-2),反比例函数y=$\frac{k}{x}$的图象经过点C,一次函数y=ax+b的图象经过A、C两点.(1)求反比例函数与一次函数的解析式;
(2)求反比例函数与一次函数的另一个交点M的坐标;
(3)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.
分析 (1)先根据A点和B点坐标得到正方形的边长,则BC=3,于是可得到C(3,-2),然后利用待定系数法求反比例函数与一次函数的解析式;
(2)通过解关于反比例函数解析式与一次函数的解析式所组成的方程组可得到M点的坐标;
(3)根据函数的图象结合交点即可求得.
解答 解:(1)∵点A的坐标为(0,1),点B的坐标为(0,-2),
∴AB=1+2=3,
∵四边形ABCD为正方形,
∴Bc=3,
∴C(3,-2),
把C(3,-2)代入y=$\frac{k}{x}$得k=3×(-2)=-6,
∴反比例函数解析式为y=-$\frac{6}{x}$,
把C(3,-2),A(0,1)代入y=ax+b得$\left\{\begin{array}{l}{3a+b=-2}\\{b=-1}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-1}\\{b=1}\end{array}\right.$,
∴一次函数解析式为y=-x+1;
(2)解方程组$\left\{\begin{array}{l}{y=-x+1}\\{y=-\frac{6}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2}\\{y=3}\end{array}\right.$,
∴M点的坐标为(-2,3);
(3)∵一次函数的值与反比例函数的图象的两个交点是M(-2,3),C(3,-2),
∴由图象可知,x的取值范围是x<-2或0<<3.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

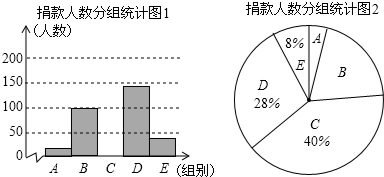
被调查的捐款人数分组统计表:
| 组别 | 捐款额x/元 | 人数 |
| A | 1≤x<10 | a |
| B | 10≤x<20 | 100 |
| C | 20≤x<30 | 200 |
| D | 30≤x<40 | 140 |
| E | 40≤x | 40 |
(1)求a的值和参与调查的总人数;
(2)补全“被调查的捐款人数分组统计图1”并计算扇形B的圆心角度数;
(3)已知该校有学生2200人,请估计捐款数不少于30元的学生人数有多少人?
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
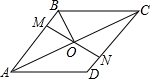 如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,MN与AC交于点O,连接DO,若∠BAC=28°,则∠ODC的度数为( )
如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,MN与AC交于点O,连接DO,若∠BAC=28°,则∠ODC的度数为( )| A. | 28° | B. | 52° | C. | 62° | D. | 72° |
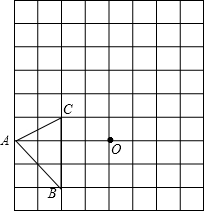 如图,在边长均为1的正方形网格纸上有一个△ABC,顶点A、B、C及点O均在格点上,请按要求完成以下操作或运算:
如图,在边长均为1的正方形网格纸上有一个△ABC,顶点A、B、C及点O均在格点上,请按要求完成以下操作或运算: