题目内容
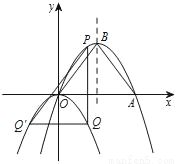
如图,抛物线y=﹣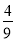 x2+bx+c经过原点和点A(6,0),与其对称轴交于点B,P是抛物线y=﹣
x2+bx+c经过原点和点A(6,0),与其对称轴交于点B,P是抛物线y=﹣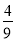 x2+bx+c上一动点,且在x轴上方.过点P作x轴的垂线交动抛物线y=﹣
x2+bx+c上一动点,且在x轴上方.过点P作x轴的垂线交动抛物线y=﹣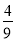 (x﹣h)2(h为常数)于点Q,过点Q作PQ的垂线交动抛物线y=﹣
(x﹣h)2(h为常数)于点Q,过点Q作PQ的垂线交动抛物线y=﹣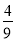 (x﹣h)2于点Q′(不与点Q重合),连结PQ′,设点P的横坐标为m.
(x﹣h)2于点Q′(不与点Q重合),连结PQ′,设点P的横坐标为m.
(1)求抛物线y=﹣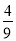 x2+bx+c的函数关系式及点B的坐标;
x2+bx+c的函数关系式及点B的坐标;
(2)当h=0时.
①求证: 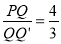 ;
;
②设△PQQ′与△OAB重叠部分图形的周长为l,求l与m之间的函数关系式;
(3)当h≠0时,是否存在点P,使四边形OAQQ′为菱形?若存在,请直接写出h的值;若不存在,请说明理由.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


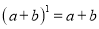 ,
,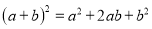 ,
,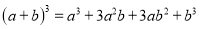 ,
,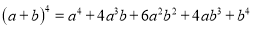 ,
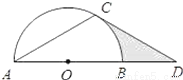
,
 ;
;  .
. B.
B. 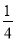 C.
C. 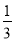 D.
D. 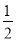
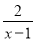 有意义,则x的取值范围是
有意义,则x的取值范围是