题目内容
10．先化简$\frac{{x}^{2}-（x-1）（x+1）}{x+1}$•$\frac{{x}^{2}-1}{x}$，再从-2、-1、0、1、$\sqrt{2}$中选一个你认为适合的数作为x的值代入求值．分析 先根据分式混合运算的法则把原式进行化简，再选取合适的x的值代入进行计算即可．
解答 解：原式=$\frac{1}{x+1}$•$\frac{（x+1）（x-1）}{x}$
=$\frac{x-1}{x}$，
当x=-2时，原式=$\frac{-2-1}{-2}$=$\frac{3}{2}$．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
4．若|a|=$\frac{5}{2}$，则a的值为（ ）
| A． | $\frac{5}{2}$ | B． | -$\frac{5}{2}$ | C． | $±\frac{5}{2}$ | D． | $\frac{2}{5}$ |
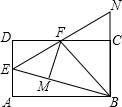如图，在矩形ABCD中，点E是AD的中点，∠EBC的平分线交CD于点F，将△DEF沿EF折叠，点D恰好落在BE上M点处，延长BC、EF交于点N，有下列四个结论：①DF=CF；②BF⊥EN；③△BEN是等边三角形；④S△BEF=3S△DEF．其中，正确的结论是①②④．
如图，小明在完成数学作业时，遇到了这样一个问题，AB=CD，BC=AD，小明动手测量了一下，发现∠A确实与∠C相等，但他不能说明其中的道理，请你帮助他说明这个道理．
19．方程mx-2y=x+5是二元一次方程，则m的值（ ）
| A． | 不可能是-1 | B． | 不可能是-2 | C． | 不可能是1 | D． | 不可能是2 |