题目内容
15.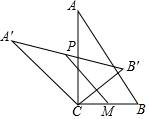 如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( )
如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 如图连接PC.思想求出PC=2,根据PM≤PC+CM,可得PM≤3,由此即可解决问题.
解答 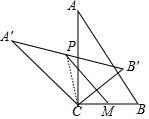 解:如图连接PC.
解:如图连接PC.
在Rt△ABC中,∵∠A=30°,BC=2,
∴AB=4,
根据旋转不变性可知,A′B′=AB=4,
∴A′P=PB′,
∴PC=$\frac{1}{2}$A′B′=2,
∵CM=BM=1,
又∵PM≤PC+CM,即PM≤3,
∴PM的最大值为3(此时P、C、M共线).
故选B.
点评 本题考查旋转变换、解直角三角形、直角三角形30度角的性质、直角三角形斜边中线定理,三角形的三边关系等知识,解题的关键是学会添加常用辅助线,学会利用三角形的三边关系解决最值问题,属于中考常考题型.

练习册系列答案
相关题目
3.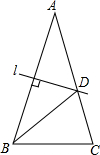 如图,在△ABC中,AB=AC,∠A=30°,AB的垂直平分线l交AC于点D,则∠CBD的度数为( )
如图,在△ABC中,AB=AC,∠A=30°,AB的垂直平分线l交AC于点D,则∠CBD的度数为( )
 如图,在△ABC中,AB=AC,∠A=30°,AB的垂直平分线l交AC于点D,则∠CBD的度数为( )
如图,在△ABC中,AB=AC,∠A=30°,AB的垂直平分线l交AC于点D,则∠CBD的度数为( )| A. | 30° | B. | 45° | C. | 50° | D. | 75° |
20.下列关于图形对称性的命题,正确的是( )
| A. | 圆既是轴对称图形,又是中心对称图形 | |
| B. | 正三角形既是轴对称图形,又是中心对称图形 | |
| C. | 线段是轴对称图形,但不是中心对称图形 | |
| D. | 菱形是中心对称图形,但不是轴对称图形 |
7.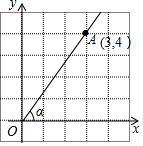 如图,在平面直角坐标系中,点A的坐标为(3,4),那么sinα的值是( )
如图,在平面直角坐标系中,点A的坐标为(3,4),那么sinα的值是( )
 如图,在平面直角坐标系中,点A的坐标为(3,4),那么sinα的值是( )
如图,在平面直角坐标系中,点A的坐标为(3,4),那么sinα的值是( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{3}$ |
4.今年世界环境日,某校组织以保护环境为主题的演讲比赛,参加决赛的6名选手成绩(单位:分)如下:8.5,8.8,9.4,9.0,8.8,9.5,这6名选手成绩的众数和中位数分别是( )
| A. | 8.8分,8.8分 | B. | 9.5分,8.9分 | C. | 8.8分,8.9分 | D. | 9.5分,9.0分 |
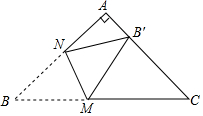 如图,在Rt△ABC中,∠A=90°,AB=AC,BC=$\sqrt{2}$+1,点M,N分别是边BC,AB上的动点,沿MN所在的直线折叠∠B,使点B的对应点B′始终落在边AC上,若△MB′C为直角三角形,则BM的长为$\frac{1}{2}$$\sqrt{2}$+$\frac{1}{2}$或1.
如图,在Rt△ABC中,∠A=90°,AB=AC,BC=$\sqrt{2}$+1,点M,N分别是边BC,AB上的动点,沿MN所在的直线折叠∠B,使点B的对应点B′始终落在边AC上,若△MB′C为直角三角形,则BM的长为$\frac{1}{2}$$\sqrt{2}$+$\frac{1}{2}$或1.