题目内容
7.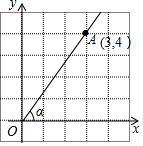 如图,在平面直角坐标系中,点A的坐标为(3,4),那么sinα的值是( )
如图,在平面直角坐标系中,点A的坐标为(3,4),那么sinα的值是( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{3}$ |
分析 作AB⊥x轴于B,如图,先利用勾股定理计算出OA=5,然后在Rt△AOB中利用正弦的定义求解.
解答 解:作AB⊥x轴于B,如图,
∵点A的坐标为(3,4),
∴OB=3,AB=4,
∴OA=$\sqrt{{3}^{2}+{4}^{2}}$=5,
在Rt△AOB中,sinα=$\frac{AB}{OA}$=$\frac{4}{5}$.
故选C.
点评 本题考查了解直角三角形:充分利用勾股定理和三角函数的定义计算三角形的边或角.也考查了坐标与图形性质.

练习册系列答案
相关题目
18.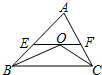 如图,在△ABC中,点O是△ABC的内心,连接OB,OC,过点O作EF∥BC分别交AB,AC于点E,F.已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )
如图,在△ABC中,点O是△ABC的内心,连接OB,OC,过点O作EF∥BC分别交AB,AC于点E,F.已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )
 如图,在△ABC中,点O是△ABC的内心,连接OB,OC,过点O作EF∥BC分别交AB,AC于点E,F.已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )
如图,在△ABC中,点O是△ABC的内心,连接OB,OC,过点O作EF∥BC分别交AB,AC于点E,F.已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )| A. | 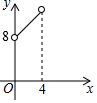 | B. | 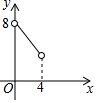 | C. | 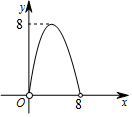 | D. | 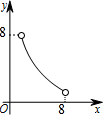 |
15.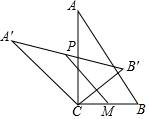 如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( )
如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( )
 如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( )
如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
12.不等式3x+6≥9的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
19. 如图,△ABC中,∠A=60°,∠B=40°,则∠C等于( )
如图,△ABC中,∠A=60°,∠B=40°,则∠C等于( )
 如图,△ABC中,∠A=60°,∠B=40°,则∠C等于( )
如图,△ABC中,∠A=60°,∠B=40°,则∠C等于( )| A. | 100° | B. | 80° | C. | 60° | D. | 40° |
17.下列哪一个是假命题( )
| A. | 五边形外角和为360° | |
| B. | 切线垂直于经过切点的半径 | |
| C. | (3,-2)关于y轴的对称点为(-3,2) | |
| D. | 抛物线y=x2-4x+2017对称轴为直线x=2 |
 如图,△ABC中,D,E分别是AB,AC的中点,连接DE.若DE=3,则线段BC的长等于6.
如图,△ABC中,D,E分别是AB,AC的中点,连接DE.若DE=3,则线段BC的长等于6.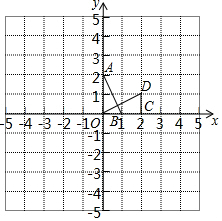 如图,在平面直角坐标系xOy中,△AOB可以看作是△OCD经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△OCD得到△AOB的过程:△OCD绕C点顺时针旋转90°,并向左平移2个单位得到△AOB.
如图,在平面直角坐标系xOy中,△AOB可以看作是△OCD经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△OCD得到△AOB的过程:△OCD绕C点顺时针旋转90°,并向左平移2个单位得到△AOB.