题目内容
5.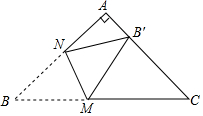 如图,在Rt△ABC中,∠A=90°,AB=AC,BC=$\sqrt{2}$+1,点M,N分别是边BC,AB上的动点,沿MN所在的直线折叠∠B,使点B的对应点B′始终落在边AC上,若△MB′C为直角三角形,则BM的长为$\frac{1}{2}$$\sqrt{2}$+$\frac{1}{2}$或1.
如图,在Rt△ABC中,∠A=90°,AB=AC,BC=$\sqrt{2}$+1,点M,N分别是边BC,AB上的动点,沿MN所在的直线折叠∠B,使点B的对应点B′始终落在边AC上,若△MB′C为直角三角形,则BM的长为$\frac{1}{2}$$\sqrt{2}$+$\frac{1}{2}$或1.
分析 ①如图1,当∠B′MC=90°,B′与A重合,M是BC的中点,于是得到结论;②如图2,当∠MB′C=90°,推出△CMB′是等腰直角三角形,得到CM=$\sqrt{2}$MB′,列方程即可得到结论.
解答  解:①如图1,
解:①如图1,
当∠B′MC=90°,B′与A重合,M是BC的中点,
∴BM=$\frac{1}{2}$BC=$\frac{1}{2}$$\sqrt{2}$+$\frac{1}{2}$;
②如图2,当∠MB′C=90°,
∵∠A=90°,AB=AC,
∴∠C=45°,
∴△CMB′是等腰直角三角形,
∴CM=$\sqrt{2}$MB′,
∵沿MN所在的直线折叠∠B,使点B的对应点B′,
∴BM=B′M,
∴CM=$\sqrt{2}$BM,
∵BC=$\sqrt{2}$+1,
∴CM+BM=$\sqrt{2}$BM+BM=$\sqrt{2}$+1,
∴BM=1,
综上所述,若△MB′C为直角三角形,则BM的长为$\frac{1}{2}$$\sqrt{2}$+$\frac{1}{2}$或1,
故答案为:$\frac{1}{2}$$\sqrt{2}$+$\frac{1}{2}$或1.
点评 本题考查了翻折变换-折叠问题,等腰直角三角形的性质,正确的作出图形是解题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
15.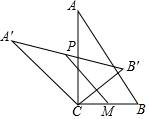 如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( )
如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( )
 如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( )
如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
20.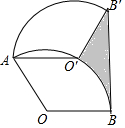 如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )
如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )
 如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )
如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )| A. | $\frac{2π}{3}$ | B. | 2$\sqrt{3}$-$\frac{π}{3}$ | C. | 2$\sqrt{3}$-$\frac{2π}{3}$ | D. | 4$\sqrt{3}$-$\frac{2π}{3}$ |
17.下列哪一个是假命题( )
| A. | 五边形外角和为360° | |
| B. | 切线垂直于经过切点的半径 | |
| C. | (3,-2)关于y轴的对称点为(-3,2) | |
| D. | 抛物线y=x2-4x+2017对称轴为直线x=2 |
3. 某住宅小区六月份1日至6日每天用水量变化情况如折线图所示,那么这6天的平均用水量是( )
某住宅小区六月份1日至6日每天用水量变化情况如折线图所示,那么这6天的平均用水量是( )
 某住宅小区六月份1日至6日每天用水量变化情况如折线图所示,那么这6天的平均用水量是( )
某住宅小区六月份1日至6日每天用水量变化情况如折线图所示,那么这6天的平均用水量是( )| A. | 30吨 | B. | 31 吨 | C. | 32吨 | D. | 33吨 |
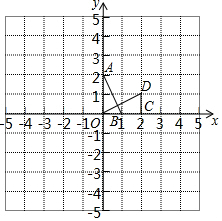 如图,在平面直角坐标系xOy中,△AOB可以看作是△OCD经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△OCD得到△AOB的过程:△OCD绕C点顺时针旋转90°,并向左平移2个单位得到△AOB.
如图,在平面直角坐标系xOy中,△AOB可以看作是△OCD经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△OCD得到△AOB的过程:△OCD绕C点顺时针旋转90°,并向左平移2个单位得到△AOB.
