题目内容
已知等腰三角形的一边长为3,另一边长为8,则它的周长是( )
| A、14 | B、19 |
| C、11 | D、14或19 |
考点:等腰三角形的性质,三角形三边关系
专题:
分析:因为已知长度为3和8两边,没有明确是底边还是腰,所以有两种情况,需要分类讨论.
解答:解:①当3为底时,其它两边都为8,
3、8、8可以构成三角形,
周长为19;
②当4为腰时,
其它两边为3和8,
∵3+3<8,
∴不能构成三角形,故舍去,
∴答案只有19.
故选B.
3、8、8可以构成三角形,
周长为19;
②当4为腰时,
其它两边为3和8,
∵3+3<8,
∴不能构成三角形,故舍去,
∴答案只有19.
故选B.
点评:本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.

练习册系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,AC=5,AB=13,则cosB的值为( )
如图,在Rt△ABC中,∠C=90°,AC=5,AB=13,则cosB的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,线段AB两个端点的坐标分别是A(6,4),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的
如图,线段AB两个端点的坐标分别是A(6,4),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的| 1 |
| 2 |
| A、(3,2) |
| B、(4,1) |
| C、(3,1) |
| D、(4,2) |
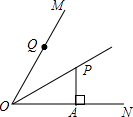 如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上一个动点,若PA=2,则PQ的最小值为( )
如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上一个动点,若PA=2,则PQ的最小值为( )| A、PQ<2 |
| B、PQ=2 |
| C、PQ>2 |
| D、以上情况都有可能 |
 如图所示,有一个形如六边形的点阵,它的中心是一个点,第二层每边有两个点,第三层每边有三个点,依此类推
如图所示,有一个形如六边形的点阵,它的中心是一个点,第二层每边有两个点,第三层每边有三个点,依此类推 如图是二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象,观察图象,当ax2+(b-m)x+c-n=0时,求x的值.
如图是二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象,观察图象,当ax2+(b-m)x+c-n=0时,求x的值.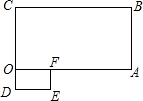 如图,矩形ODEF的一边落在矩形ABCO的一边上,并且矩形ODEF∽矩形ABCO,其相似比为1:4,矩形ABCO的边AB=4,BC=4
如图,矩形ODEF的一边落在矩形ABCO的一边上,并且矩形ODEF∽矩形ABCO,其相似比为1:4,矩形ABCO的边AB=4,BC=4