题目内容
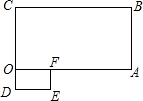 如图,矩形ODEF的一边落在矩形ABCO的一边上,并且矩形ODEF∽矩形ABCO,其相似比为1:4,矩形ABCO的边AB=4,BC=4
如图,矩形ODEF的一边落在矩形ABCO的一边上,并且矩形ODEF∽矩形ABCO,其相似比为1:4,矩形ABCO的边AB=4,BC=4| 3 |
考点:相似多边形的性质,旋转的性质
专题:
分析:先根据相似多边形对应边的比相等的性质求出OF=
,OD=1,由勾股定理得到OE=
=2,将矩形ODEF绕点O逆时针旋转一周,点E的轨迹是以点O为圆心以2为半径的圆,所以△ACE的AC边上的高就是点E到AC的距离,也就是AC到圆上的点的距离,最大值为点O到AC的距离与圆的半径的和,再利用三角形的面积公式求解即可.
| 3 |
| OF2+OD2 |
解答:解:∵矩形ODEF∽矩形ABCO,其相似比为1:4,矩形ABCO的边AB=4,BC=4
,
∴OF=
,OD=1,
∴OE=
=
=2,
所以点E的轨迹为以点O为圆心,以2为半径的圆,
设点O到AC的距离为h,
AC=
=
=8,
∴8h=4×4
,
解得h=2
,
∴当点E到AC的距离为2
+2时,△ACE的面积有最大值,
S最大=
×8(2
+2)=8
+8.
故答案为8
+8.
| 3 |
∴OF=
| 3 |
∴OE=
| OF2+OD2 |
(
|
所以点E的轨迹为以点O为圆心,以2为半径的圆,
设点O到AC的距离为h,
AC=
| AB2+BC2 |
42+(4
|
∴8h=4×4
| 3 |
解得h=2
| 3 |
∴当点E到AC的距离为2
| 3 |
S最大=
| 1 |
| 2 |
| 3 |
| 3 |
故答案为8
| 3 |
点评:本题主要考查了相似多边形的性质,矩形的性质,勾股定理,圆上的点到直线的距离的取值范围,理解AC边上的高的最大值为点O到AC的距离与圆的半径的和是解本题的关键.

练习册系列答案
相关题目
在
、-
、-
、
中最大的数是( )
| 1 | |||
|
| 3 | 0.001 |
| 0.01 |
| 1 | ||
-
|
A、
| |||||
B、-
| |||||
C、-
| |||||
D、
|
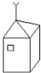 如图所示,从正面看,所能看到的结果是图形( )
如图所示,从正面看,所能看到的结果是图形( )A、 |
B、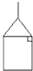 |
C、 |
D、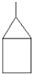 |
已知等腰三角形的一边长为3,另一边长为8,则它的周长是( )
| A、14 | B、19 |
| C、11 | D、14或19 |
下列说法中,正确的是( )
| A、整数就是正整数和负整数 |
| B、-a一定是负数 |
| C、+5是表示向东走5米 |
| D、零既不是正数,也不是负数 |
 如图,⊙O的直径AB与弦CD相交,∠ACD=60°,则∠BAD=
如图,⊙O的直径AB与弦CD相交,∠ACD=60°,则∠BAD=