题目内容
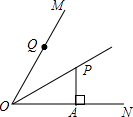如图，OP平分∠MON，PA⊥ON于点A，点Q是射线OM上一个动点，若PA=2，则PQ的最小值为（ ）| A、PQ＜2 |
| B、PQ=2 |
| C、PQ＞2 |
| D、以上情况都有可能 |
考点：角平分线的性质,垂线段最短
专题：
分析：根据垂线段最短判断出PQ⊥OM时，PQ的值最小，再根据角平分线上的点到角的两边距离相等可得PQ=PA．
解答：解：由垂线段最短可得PQ⊥OM时，PQ的值最小，
∵OP平分∠MON，PA⊥ON，
∴PQ的最小值=PA=2．
故选B．
∵OP平分∠MON，PA⊥ON，
∴PQ的最小值=PA=2．
故选B．
点评：本题考查了角平分线上的点到角的两边距离相等的性质，垂线段最短，熟记性质是解题的关键．
练习册系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
已知等腰三角形的一边长为3，另一边长为8，则它的周长是（ ）
| A、14 | B、19 |
| C、11 | D、14或19 |
下列式子：x2+2，
+4，
，
，-5x，0中，整式的个数有（ ）
| 1 |
| a |
| 3ab |
| 7 |
| ab |
| c |
| A、3个 | B、4个 | C、5个 | D、6个 |
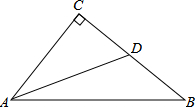已知在△ABC中，∠C=90°，D点在BC边上，且BD=