题目内容
20.下列计算正确的是( )| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | 4$\sqrt{3}-3\sqrt{3}$=1 | C. | 2$\sqrt{3}×3\sqrt{3}=6\sqrt{3}$ | D. | $\sqrt{27}÷\sqrt{3}=3$ |
分析 根据二次根式的加减法对A、B进行判断;根据二次根式的乘法法则对C进行判断;根据二次根式的除法法则对D进行判断.
解答 解:A、$\sqrt{2}$与$\sqrt{3}$不能合并,所以A选项错误;
B、原式=$\sqrt{3}$,所以B选项错误;
C、原式=6×3=18,所以C选项错误;
D、原式=$\sqrt{27÷3}$=3,所以D选正确.
故选D.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
10.下列各数中为无理数的是( )
| A. | $\sqrt{16}$ | B. | 3.14 | C. | 0.$\stackrel{•}{3}$ | D. | $-\frac{π}{2017}$ |
8.关于x的一元二次方程x2-6x+k=0有两个不相等的实数根,则实数k的取值范围是( )
| A. | k≤9 | B. | k<9 | C. | k≥9 | D. | k>9 |
5. 如图,某小区有一块长为18m,宽为6m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为60m2,两块绿地之间及周边留有宽度相等的人形通道,若设人形道的宽度为xm,则可以列出关于x的方程是( )
如图,某小区有一块长为18m,宽为6m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为60m2,两块绿地之间及周边留有宽度相等的人形通道,若设人形道的宽度为xm,则可以列出关于x的方程是( )
 如图,某小区有一块长为18m,宽为6m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为60m2,两块绿地之间及周边留有宽度相等的人形通道,若设人形道的宽度为xm,则可以列出关于x的方程是( )
如图,某小区有一块长为18m,宽为6m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为60m2,两块绿地之间及周边留有宽度相等的人形通道,若设人形道的宽度为xm,则可以列出关于x的方程是( )| A. | x2+9x-8=0 | B. | x2-9x+8=0 | C. | x2-9x-8=0 | D. | 2x2-9x+8=0 |
12. 某学校拟建一间矩形活动室,一面靠墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,建成后的活动室面积为75m2,求矩形活动室的长和宽,若设矩形宽为x,根据题意可列方程为( )
某学校拟建一间矩形活动室,一面靠墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,建成后的活动室面积为75m2,求矩形活动室的长和宽,若设矩形宽为x,根据题意可列方程为( )
 某学校拟建一间矩形活动室,一面靠墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,建成后的活动室面积为75m2,求矩形活动室的长和宽,若设矩形宽为x,根据题意可列方程为( )
某学校拟建一间矩形活动室,一面靠墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,建成后的活动室面积为75m2,求矩形活动室的长和宽,若设矩形宽为x,根据题意可列方程为( )| A. | x(27-3x)=75 | B. | x(3x-27)=75 | C. | x(30-3x)=75 | D. | x(3x-30)=75 |
10.当x( )时,分式$\frac{x+1}{1+\frac{4}{x+2}}$有意义.
| A. | 等于-2 | B. | 不等于-2 | C. | 等于-2或-6 | D. | ≠2和-6 |
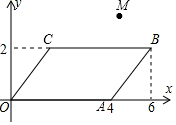 如图,在平面直角坐标系xOy中,四边形OABC是平行四边形,且A(4,0)、B(6,2)、M(4,3).在平面内有一条过点M的直线将平行四边形OABC的面积分成相等的两部分,请写出该直线的函数表达式y=2x-5.
如图,在平面直角坐标系xOy中,四边形OABC是平行四边形,且A(4,0)、B(6,2)、M(4,3).在平面内有一条过点M的直线将平行四边形OABC的面积分成相等的两部分,请写出该直线的函数表达式y=2x-5.


