题目内容
4.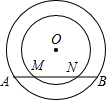 如图,同心⊙O中,大圆弦AB与小圆交于点M、N.
如图,同心⊙O中,大圆弦AB与小圆交于点M、N.(1)求证:AM=BN;
(2)若AB=8,MN=4,且大圆半径为5,求小圆的半径.
分析 (1)过O作OE⊥AB,根据垂径定理得到AE=BE,ME=NE,从而得到AM=BN;
(2)由(1)可知,OE⊥AB且OE⊥NM,连接OM,OA,再根据勾股定理求出OE及OM的长即可.
解答 解:(1)如图1所示:过点E作OE⊥AB,垂足为E.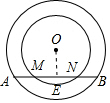
图1
∵OA⊥AB,
∴AE=BE,ME=NE.
∴AE-ME=EB-NE,即AM=NB.
(2)如图2所示: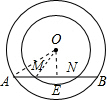
图2
∵AE=BE,AB=8,
∴AE=4.
又∵AO=5,
∴OE=$\sqrt{O{A}^{2}-A{E}^{2}}$=3.
∵ME=NE,MN=4,
∴ME=2.
∴OM=$\sqrt{O{E}^{2}+M{E}^{2}}$=$\sqrt{13}$.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
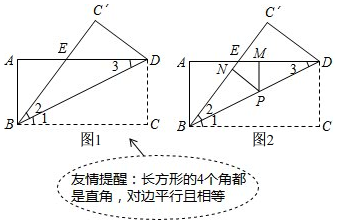
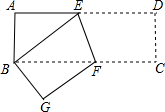 如图,在矩形纸片ABCD中,AD=9,AB=3,将其折叠,使点D与点B重合,折痕为EF,求折叠后DE的长和折痕EF的长.
如图,在矩形纸片ABCD中,AD=9,AB=3,将其折叠,使点D与点B重合,折痕为EF,求折叠后DE的长和折痕EF的长.
 如图,点O是直线l上一点,作射线OA,过O点作OB⊥OA于点O,则图中∠1,∠2的数量关系为∠1+∠2=90°.
如图,点O是直线l上一点,作射线OA,过O点作OB⊥OA于点O,则图中∠1,∠2的数量关系为∠1+∠2=90°.