题目内容

13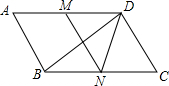．如图，在?ABCD中，∠C=60°，M、N分别是AD、BC的中点，BC=2CD
（1）求证：四边形MNCD是平行四边形；
（2）连接DN，求证：MN=DN．

分析 （1）利用“有一组对边平行且相等的四边形为平行四边形”证得结论；
（2）根据已知条件判定△CDN为等边三角形，利用等边三角形的性质和平行四边形的性质证得结论．

解答 证明：（1）∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
又∵M、N分别是AD、BC的中点，
∴DM∥CN，DM=CN，
∴四边形MNCD是平行四边形；

（2）由（1）知，四边形MNCD是平行四边形，则MN=CD．
∵BC=2CD，BC=2CN，
∴CD=CN．
又∵∠C=60°，
∴△CDN为等边三角形，
∴DN=CD，
∴MN=DN．

点评 本题考查了平行四边形的判定与性质．平行四边形的判定方法共有五种，应用时要认真领会它们之间的联系与区别，同时要根据条件合理、灵活地选择方法．

练习册系列答案
相关题目
3．如图1，点E为正方形ABCD的边AB上一点，EF⊥EC，且EF=EC，连接AF．
（1）求∠EAF的度数；
（2）如图2，连接FC交BD于M，交AD于N．
①求证：$\sqrt{2}$AD=AF+2DM；
②若AF=10$\sqrt{2}$，AN=12，则MD的长为$\frac{5\sqrt{2}}{2}$．
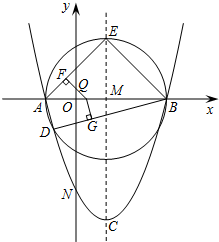4．已知：抛物线y=ax2+bx+c（a≠0），顶点C（1，-4），与x轴交于A、B两点，与y轴交于点N（0，-3）．
（1）求这条抛物线的解析式；
（2）如图，以AB为直径作⊙M，与抛物线交于点D，与抛物线的对称轴交于点E，依次连接A、D、B、E，点Q为线段AB上一个动点（Q与A、B两点不重合），过点Q作QF⊥AE于F，QG⊥DB于G，请判断$\frac{QF}{BE}+\frac{QG}{AD}$是否为定值？若是，请求出此定值；若不是，请说明理由；
（3）请求出抛物线与（2）中⊙M的所有交点坐标．
1．如图，在△ABC中，E为BC中点，AD平分∠BAC，EF∥AD，EF与AC的延长线交于点F，与AB交于H，试说明：BH=CF．
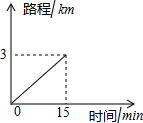8．小丽家离学校2km，步行到校需30min，小丽的同学小军上学要经过小丽家，小军骑车上学行驶的路程与时间的关系如图所示．
（1）小军家离学校多远？骑车上学的平均速度是多少？
（2）如果小丽与小军同时从家里出发上学，试在小军上学的路程与时间的关系图上画出小丽上学的路程与时间的关系图．
（3）他们同时从家里出发，途中能相遇吗？
18．如图1，△ABC中，AB=AC，点O是BC的中点，以O为圆心的⊙O与AB边相切于点D．
（1）判断AC边与⊙O的位置关系，说明理由；
（2）如图2，若AB=5，BC=6，点F为⊙O上一动点，过点F作⊙O的切线分别交AD边、AC边于点G、H，连结OG、OH．
①设∠BAC=α，则∠GOH=90°-$\frac{1}{2}$α（用含α的代数式表示）；
②若△OGH是以GH为腰的等腰三角形，求BG的长．
5．将一个三角形平均分成面积相等的6块，请问有几种切法？其中切三刀的切法有几种？
2．已知点M（2，1）在二次函数y=ax2-2bx+1的图象上．
（1）b=a；（用含a的代数式表示）；
（2）该二次函数的图象与x轴的两个交点为A、B，若AB=1，求该二次函数的表达式；
（3）在（2）的条件下，若A（m，y1），B（m+2，y2）两点都在该函数的图象上，试探究y1与y2的大小．
3．如图，相邻两线段互相垂直，两只蜗牛均同时从A点出发爬往C点，蜗牛甲沿着“A→B→C”路线走，蜗牛乙沿着“A→D→E→F→G→H→I→J→C”的路线走，若他们的爬行速度相同，则先到达点C的是（　　）
A．蜗牛甲B．蜗牛乙C．同时到达D．无法确定

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网