题目内容
4.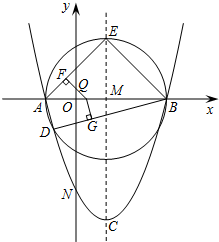 已知:抛物线y=ax2+bx+c(a≠0),顶点C(1,-4),与x轴交于A、B两点,与y轴交于点N(0,-3).
已知:抛物线y=ax2+bx+c(a≠0),顶点C(1,-4),与x轴交于A、B两点,与y轴交于点N(0,-3).(1)求这条抛物线的解析式;
(2)如图,以AB为直径作⊙M,与抛物线交于点D,与抛物线的对称轴交于点E,依次连接A、D、B、E,点Q为线段AB上一个动点(Q与A、B两点不重合),过点Q作QF⊥AE于F,QG⊥DB于G,请判断$\frac{QF}{BE}+\frac{QG}{AD}$是否为定值?若是,请求出此定值;若不是,请说明理由;
(3)请求出抛物线与(2)中⊙M的所有交点坐标.
分析 (1)可将抛物线的解析式设为顶点式,然后将N点坐标代入,即可求得抛物线的解析式;
(2)根据两对相似三角形:△AQF、△ABE和△BGQ、△BDA得出的对应成比例线段,即可求出所求的代数式是否为定值;
(3)过点D作DN⊥AB,垂足为N,令y=0得:x2-2x-3=0,解得:x1=3,x2=-1,可知点A(-1,0)、点B(3,0),设点D的坐标为(m,m2-2m-3),然后证明△ADN∽△DBN,利用相似三角形的性质可知$\frac{AN}{DN}=\frac{DN}{BN}$,即:$\frac{m+1}{-{(m}^{2}-2m-3)}=\frac{-({m}^{2}-2m-3)}{3-m}$,从而可解得m的值,从而可求得点D的坐标为(1-$\sqrt{3}$,-1),点D′的坐标为(1+$\sqrt{3}$,-1).
解答 解:(1)设抛物线的解析式为y=a(x-1)2-4,
将N(0,-3)代入解析式得:-3=a(0-1)2-4,
∴a=1,
∵抛物线的解析式为y=(x-1)2-4,即y=x2-2x-3;
(2)是定值:$\frac{QF}{BE}+\frac{QG}{AD}$=1,
理由:∵AB是直径,
∴∠AEB=90°,
∵QF⊥AE,
∴QF∥BE,
∴△AQF∽△ABE,
∴$\frac{QF}{BE}$=$\frac{AQ}{AB}$,
同理:$\frac{QG}{AD}$=$\frac{QB}{AB}$,
∴$\frac{QF}{BE}+\frac{QG}{AD}$=$\frac{AQ}{AB}+\frac{QB}{AB}$=$\frac{AQ+QB}{AB}$=$\frac{AB}{AB}$=1;
(3)如图所示,过点D作DN⊥AB,垂足为N.
令y=0得:x2-2x-3=0,解得:x1=3,x2=-1,
∴点A的坐标为(-1,0)、点B的坐标为(3,0).
设点D的坐标为(m,m2-2m-3),
∵AB是直径,
∴∠ADB=90°.
∴∠ADN+∠NDB=90°.
∵∠NDB+∠DBN=90°,
∴∠ADN=∠DBN.
又∵∠AND=∠BND=90°,
∴△ADN∽△DBN.
∴$\frac{AN}{DN}=\frac{DN}{BN}$,即:$\frac{m+1}{-{(m}^{2}-2m-3)}=\frac{-({m}^{2}-2m-3)}{3-m}$
解得:m1=-1(舍去),m2=3(舍去),${m}_{3}=1-\sqrt{3}$,${m}_{4}=1+\sqrt{3}$.
当m=1-$\sqrt{3}$时,m2-2m-3=$(1-\sqrt{3})^{2}-2(1-\sqrt{3})-3$=1,
当m=1+$\sqrt{3}$时,m2-2m-3=$(1+\sqrt{3})^{2}-2(1+\sqrt{3})-3$=1.
∴点D的坐标为(1-$\sqrt{3}$,-1),点D′的坐标为(1+$\sqrt{3}$,-1).
综上所述,抛物线与圆的交点坐标分别为A(-1,0)、B(3,0)、D(1-$\sqrt{3}$,-1)、D′(1+$\sqrt{3}$,-1).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了相似三角形的性质、圆的性质和二次函数的性质和因式分解法-解方程.设设点D的坐标为(m,m2-2m-3),然后证得△ADN∽△DBN,利用相似三角形的性质得到关于m的方程,然后解得m的值是解题的关键.

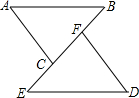 如图,△ABC与△DEF是全等三角形,即△ABC≌△DEF,那么图中相等的线段有( )
如图,△ABC与△DEF是全等三角形,即△ABC≌△DEF,那么图中相等的线段有( )| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
 如图,函数y1=ax+b与函数y2=cx+d相交于点A,点A的横坐标为1,若t=y1-y2,则令t>0的x的取值范围是x>1.
如图,函数y1=ax+b与函数y2=cx+d相交于点A,点A的横坐标为1,若t=y1-y2,则令t>0的x的取值范围是x>1. 如图,?DEFG内接于△ABC,已知△ADE、△EFC、△DBG的面积分别为1,2.8和1.2,则?DEFG的面积是4.
如图,?DEFG内接于△ABC,已知△ADE、△EFC、△DBG的面积分别为1,2.8和1.2,则?DEFG的面积是4.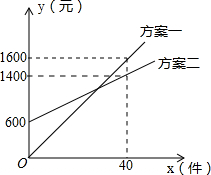 某销售公司推销一种产品,设x(种)是推销产品的数量,y(元)是付给推销员的月报酬.公司付给推销员的月报酬的两种方案如图所示,推销员可以任选一种与公司签订合同,看图解答下列问题:
某销售公司推销一种产品,设x(种)是推销产品的数量,y(元)是付给推销员的月报酬.公司付给推销员的月报酬的两种方案如图所示,推销员可以任选一种与公司签订合同,看图解答下列问题: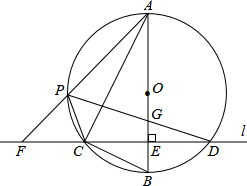 如图,在⊙O的内接△ABC中,∠ACB=90°,tan∠CAB=$\frac{1}{2}$,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是$\widehat{AC}$上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.
如图,在⊙O的内接△ABC中,∠ACB=90°,tan∠CAB=$\frac{1}{2}$,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是$\widehat{AC}$上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.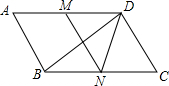 如图,在?ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD
如图,在?ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD