题目内容
1. 如图,在△ABC中,E为BC中点,AD平分∠BAC,EF∥AD,EF与AC的延长线交于点F,与AB交于H,试说明:BH=CF.
如图,在△ABC中,E为BC中点,AD平分∠BAC,EF∥AD,EF与AC的延长线交于点F,与AB交于H,试说明:BH=CF.
分析 如图,过点B作BG∥EF,交CF的延长线于点G;于是得到$\frac{AF}{FG}=\frac{AH}{HB}$,由于AD平分∠BAC,AD∥EF,推出∠BAD=∠CAD,∠BAD=∠AFH,∠AHF=∠BAD,求得∠AFH=∠AHF,根据等腰三角形的性质得到AH=AF,等量代换得到FG=HB;即可得到结论.
解答  解:如图,过点B作BG∥EF,交CF的延长线于点G;
解:如图,过点B作BG∥EF,交CF的延长线于点G;
∴$\frac{AF}{FG}=\frac{AH}{HB}$,
∵AD平分∠BAC,AD∥EF,
∴∠BAD=∠CAD,∠BAD=∠AFH,∠AHF=∠BAD,
∴∠AFH=∠AHF,
∴AH=AF,
∴FG=HB;
而EF∥BG,BE=CE,
∴CF=FG,
∴BH=CF.
点评 本题主要考查了角平分线的性质、平行线分线段成比例定理、等腰三角形的判定等知识点及其应用问题;解题的关键是作辅助线;灵活运用平行线分线段成比例定理来分析、判断、推理或解答.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
9.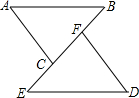 如图,△ABC与△DEF是全等三角形,即△ABC≌△DEF,那么图中相等的线段有( )
如图,△ABC与△DEF是全等三角形,即△ABC≌△DEF,那么图中相等的线段有( )
 如图,△ABC与△DEF是全等三角形,即△ABC≌△DEF,那么图中相等的线段有( )
如图,△ABC与△DEF是全等三角形,即△ABC≌△DEF,那么图中相等的线段有( )| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
11.下列式子中是二次根式的是( )
| A. | $\sqrt{7}$ | B. | $\root{3}{7}$ | C. | $\sqrt{x}$ | D. | $\sqrt{-7}$ |
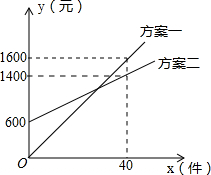 某销售公司推销一种产品,设x(种)是推销产品的数量,y(元)是付给推销员的月报酬.公司付给推销员的月报酬的两种方案如图所示,推销员可以任选一种与公司签订合同,看图解答下列问题:
某销售公司推销一种产品,设x(种)是推销产品的数量,y(元)是付给推销员的月报酬.公司付给推销员的月报酬的两种方案如图所示,推销员可以任选一种与公司签订合同,看图解答下列问题:
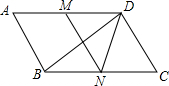 如图,在?ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD
如图,在?ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD