题目内容
7.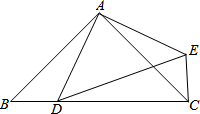 如图,△ABC是等腰直角三角形,AB=$4\sqrt{2}$,D为斜边BC上的一点(D与B、C均不重合),连结AD,把△ABD绕点A按逆时针旋转后得到△ACE,连结DE,设BD=x.
如图,△ABC是等腰直角三角形,AB=$4\sqrt{2}$,D为斜边BC上的一点(D与B、C均不重合),连结AD,把△ABD绕点A按逆时针旋转后得到△ACE,连结DE,设BD=x.(1)求证:∠DCE=90°;
(2)当△DCE的面积为6时,求x的值;
(3)当D在斜边BC上运动时(D与B、C均不重合)四边形ADCE的面积S是否随着x的变化而变化?若变化,请求出S与x之间的函数关系式;若不变,求出S的值.
分析 (1)△ABC是等腰直角三角形,△ABD绕点A按逆时针旋转后得到△ACE,得到∠ABD与∠ACE相等,进而得到∠ACE+∠ACD=90°即证得;
(2)由直角三角形到△ACE≌△ABD,从而得直角三角形的面积公式而解得;
(3)根据旋转的性质得出△ABD的面积等于△ACE的面积,进而解答即可.
解答 解:(1)∵△ABD绕点A按逆时针旋转后得到△ACE,
∴△ACE≌△ABD,
∴∠ABD=∠ACE,
又∵△ABC是等腰直角三角形,且BC为斜边,
∴∠ABD+∠ACD=90°,
∴∠ACE+∠ACD=90°,
即:∠DCE=90°;
(2)∵AC=AB=4$\sqrt{2}$,
∴BC2=AC2+AB2=$(4\sqrt{2})^{2}+(4\sqrt{2})^{2}=64$,
∴BC=8,
∵△ACE≌△ABD,∠DCE=90°,
∴CE=BD=x,而BC=8,
∴DC=8-x,
∴Rt△DCE的面积为:$\frac{1}{2}$DC•CE=$\frac{1}{2}$(8-x)x.
∴$\frac{1}{2}$(8-x)x=6,
即-x2+8x-12=0.
解得x=2或x=6;
(3)因为△ACE≌△ABD,
所以△ABD的面积等于△ACE的面积,
所以四边形ADCE的面积S不变,
S=$\frac{1}{2}×4\sqrt{2}×4\sqrt{2}$=16.
点评 本题主要考查了全等三角形的判定与性质,及一元二次方程、二次函数等基础知识,考查等价转换思想,运算求解等能力和创新意识等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.已知∠AOB=70°,∠BOC=30°,OM平分AOB,ON平分∠BOC,则∠MON=( )
| A. | 50° | B. | 20° | C. | 20°或50° | D. | 不能确定 |
3.已知菱形ABCD的边长为5,中心为O,且OA,OB的长是关于x的方程x2+(2m+1)x+m2-4=0的两个实数根,则m的值为( )
| A. | -4 | B. | 2 | C. | -4或2 | D. | 以上都不对 |
19.六边形的内角和与外角和的度数分别是( )
| A. | 1080°,180° | B. | 1080°,360° | C. | 720°,180° | D. | 720°,360° |
17.下列的计算正确的是( )
| A. | 3a-2a=1 | B. | x+2x2=3x3 | C. | -(m-n)=-m+n | D. | 3(x+2y)=3x+2y |
 已知图1、图2、图3都是4×5的方格纸,其中每个小正方形的边长均为1cm,每个小正方形的顶点称为格点.
已知图1、图2、图3都是4×5的方格纸,其中每个小正方形的边长均为1cm,每个小正方形的顶点称为格点.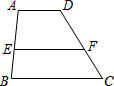 四边形ABCD中,E、F分别为AB、CD上的点,且AD∥EF∥BC,AE:EB=3:2,AD=2cm,BC=4cm,则EF=$\frac{16}{5}$cm.
四边形ABCD中,E、F分别为AB、CD上的点,且AD∥EF∥BC,AE:EB=3:2,AD=2cm,BC=4cm,则EF=$\frac{16}{5}$cm.