题目内容
9. 某学校开展“科技创新大赛”活动,设计遥控车沿直线轨道做匀速直线运动的模型.现在甲、乙两车同时分别从不同起点A,B出发,沿同一轨道到达C处.设t(分)后甲、乙两遥控车与B处的距离分别为d1,d2,且d1,d2与t的函数关系如图,若甲的速度是乙的速度的1.5倍,试根据图象解决下列问题:
某学校开展“科技创新大赛”活动,设计遥控车沿直线轨道做匀速直线运动的模型.现在甲、乙两车同时分别从不同起点A,B出发,沿同一轨道到达C处.设t(分)后甲、乙两遥控车与B处的距离分别为d1,d2,且d1,d2与t的函数关系如图,若甲的速度是乙的速度的1.5倍,试根据图象解决下列问题:(1)填空:乙的速度是40 米/分;
(2)写出d1与t的函数关系式;
(3)若甲、乙两遥控车的距离超过20米时信号不会产生相互干扰,试探求什么时间两遥控车的信号会产生相互干扰?
分析 (1)根据速度=路程÷时间,计算即可.
(2)分两种情形利用待定系数法求出分段函数的解析式即可.
(3)分两种情形,列出不等式,解不等式即可.
解答 解:(1)乙的速度=120÷3=40(米/分),
故答案为:40;
(2)由图象a=1,设函数解析式为d1=kt+b,
0≤t≤1时,把(0,60)和(1,0)代入得d1=-60t+60,
1<t≤3时,把(1,0)和(3,120)代入得d1=60t-60;
综上所述,d1=$\left\{\begin{array}{l}{-60t+60}&{(0≤t≤1)}\\{60t-60}&{(1<t≤3)}\end{array}\right.$.
(3)d2=40t,
当0≤t<1时,d2+d1>20,
即-60t+60+40t>20,解得0≤t<2,
∵0≤t<1,
∴当0≤t<1时,两遥控车的信号不会产生相互干扰;
当1≤t≤3时,d2-d1>20,即40t-(60t-60)>20,
∴1<t<2,
当2≤t≤3时,两遥控车的信号会产生相互干扰.
点评 本题考查一次函数的应用、一元一次不等式等知识,解题的关键是少林足球待定系数法确定函数解析式,学会利用不等式解决实际问题,属于中考常考题型.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
18.某校“棋乐无穷”社团前两次购买的两种材质的象棋采购如下表(近期两种材质象棋的售价一直不变);
(1)若该社团计划再采购这两种材质的象棋各5盒,则需要多少元?
(2)若该社团准备购买这两种材质的象棋共50盒,且要求塑料象棋的数量不多于玻璃象棋数量的3倍,请设计出最省钱的购买方案,并说明理由.
| 塑料象棋 | 玻璃象棋 | 总价(元) | |
| 第一次(盒) | 1 | 3 | 26 |
| 第二次(盒) | 3 | 2 | 29 |
(2)若该社团准备购买这两种材质的象棋共50盒,且要求塑料象棋的数量不多于玻璃象棋数量的3倍,请设计出最省钱的购买方案,并说明理由.
19.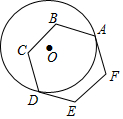 如图,半径为1的⊙O与正六边形ABCDEF相切于点A、D,则$\widehat{AD}$的长为( )
如图,半径为1的⊙O与正六边形ABCDEF相切于点A、D,则$\widehat{AD}$的长为( )
 如图,半径为1的⊙O与正六边形ABCDEF相切于点A、D,则$\widehat{AD}$的长为( )
如图,半径为1的⊙O与正六边形ABCDEF相切于点A、D,则$\widehat{AD}$的长为( )| A. | $\frac{1}{6}$π | B. | $\frac{1}{3}$π | C. | $\frac{2}{3}$π | D. | $\frac{5}{6}$π |
 如图,矩形ABCD中,AB=6,CB=18,若将矩形折叠使B与D重合,则折痕EF的长为2$\sqrt{10}$.
如图,矩形ABCD中,AB=6,CB=18,若将矩形折叠使B与D重合,则折痕EF的长为2$\sqrt{10}$. 如图,已知?OABC的顶点A、C分别在直线x=2和x=6上,O是坐标原点,则对角线OB长的最小值为8.
如图,已知?OABC的顶点A、C分别在直线x=2和x=6上,O是坐标原点,则对角线OB长的最小值为8. 实数a、b在数轴上对应的如图所示,化简$\sqrt{a^2}$-$\sqrt{b^2}$+$\sqrt{{{({a-b})}^2}}$=-2a.
实数a、b在数轴上对应的如图所示,化简$\sqrt{a^2}$-$\sqrt{b^2}$+$\sqrt{{{({a-b})}^2}}$=-2a. 如图,在△ABC中,∠A=80°,∠B=40°.D、E分别是AB,AC上的点,且DE∥BC,求∠AED的度数,说明理由.
如图,在△ABC中,∠A=80°,∠B=40°.D、E分别是AB,AC上的点,且DE∥BC,求∠AED的度数,说明理由.