题目内容
 如图,在△ABC中,AB=AC=10,BC=12,点E,F分别在边BC、AC上(点F不与点A、C重合)EF∥AB.把△ABC沿直线EF翻折,点C与点D重合,设FC=x.
如图,在△ABC中,AB=AC=10,BC=12,点E,F分别在边BC、AC上(点F不与点A、C重合)EF∥AB.把△ABC沿直线EF翻折,点C与点D重合,设FC=x.(1)求∠B的余切值;
(2)当点D在△ABC的外部时,DE、DF分别交AB于M、N,若MN=y,求y关于x的函数关系式并写出定义域;
(3)(下列所有问题只要直接写出结果即可)以E为圆心、BE长为半径的⊙E与边AC.
①没有公共点时,求x的取值范围;
②一个公共点时,求x的取值范围;
③两个公共点时,求x的取值范围.
考点:相似形综合题
专题:
分析:(1)作AH⊥BC,垂足为H,先求出BH,再根据勾股定理求出AH,即可得出结果;
(2)先求出EC=
x,BE=12-
x,再求出ME=BE=12-
x,DM=DE-ME=
x-12,然后由EF∥MN,得出比例式
=
,即可求出y=2x-10,(5<x<10);
(3)根据题意即可得出结果.
(2)先求出EC=
| 6 |
| 5 |
| 6 |
| 5 |
| 6 |
| 5 |
| 12 |
| 5 |
| DM |
| DE |
| MN |
| EF |
(3)根据题意即可得出结果.
解答:解:(1)作AH⊥BC,垂足为H,如图1所示: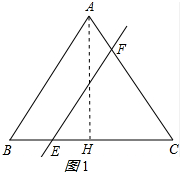
∵AB=AC=10,BC=12,
∴BH=CH=6,
∴AH=
=8,
∴cotB=
=
=
;
(2)如图2所示: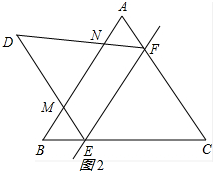
∵EF∥AB,
∴
=
,
即
=
,
∴EC=
x,
∴BE=12-
x,
∵∠CEF=∠DEF,EF∥AB,
∴∠BME=∠DEF,∠CEF=∠B,
∴∠BME=∠B,
∴ME=BE=12-
x,
∴DM=DE-ME=
x-12,
∵EF∥MN,
∴
=
,
即
=
,
∴y=2x-10,(5<x<10);
(3)①当0<x<
或
<x<10时,⊙E与边AC没有公共点;
②当x=
或
≤x<5时,⊙E与边AC有一个公共点;
③当5≤x<
时,⊙E与边AC有两个公共点.

∵AB=AC=10,BC=12,
∴BH=CH=6,
∴AH=
| 102-62 |
∴cotB=
| BH |
| AH |
| 6 |
| 8 |
| 3 |
| 4 |
(2)如图2所示:

∵EF∥AB,
∴
| EC |
| BC |
| FC |
| AC |
即
| EC |
| 12 |
| x |
| 10 |
∴EC=
| 6 |
| 5 |
∴BE=12-
| 6 |
| 5 |
∵∠CEF=∠DEF,EF∥AB,
∴∠BME=∠DEF,∠CEF=∠B,
∴∠BME=∠B,
∴ME=BE=12-
| 6 |
| 5 |
∴DM=DE-ME=
| 12 |
| 5 |
∵EF∥MN,
∴
| DM |
| DE |
| MN |
| EF |
即
| ||
|
| y |
| x |
∴y=2x-10,(5<x<10);
(3)①当0<x<
| 55 |
| 18 |
| 50 |
| 9 |
②当x=
| 50 |
| 9 |
| 55 |
| 18 |
③当5≤x<
| 50 |
| 9 |
点评:本题考查了勾股定理、相似三角形的判定与性质、三角函数以及圆的切线等知识;构造直角三角形求三角函数和由平行线得出比例式是解题的关键.

练习册系列答案
相关题目
根据下列已知条件,能唯一画出△ABC的是( )
| A、AB=5,BC=3,AC=8 |
| B、AB=4,BC=3,∠A=30° |
| C、∠C=90°,AB=6 |
| D、∠A=60°,∠B=45°,AB=4 |
若方程x2-3x-1=0的两根为x1,x2,则
的值为( )
| x1+x 2 |
| x1x2 |
| A、3 | ||
| B、-3 | ||
C、
| ||
D、-
|
如果
a3xby与-a2ybx+1的和是单项式,则x+y的值是( )
| 1 |
| 2 |
| A、1 | B、5 | C、-5 | D、-1 |
 已知:如图,数轴上线段AB=2(单位长度),线段CD=4(单位长度),点A在数轴上表示的数是-10,点C在数轴上表示的数是16.若线段AB以每秒6个单位长度的速度向右匀速运动,同时线段CD以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒.
已知:如图,数轴上线段AB=2(单位长度),线段CD=4(单位长度),点A在数轴上表示的数是-10,点C在数轴上表示的数是16.若线段AB以每秒6个单位长度的速度向右匀速运动,同时线段CD以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒. 如图,若∠BAC=∠1,则
如图,若∠BAC=∠1,则 如图,二次函数y=x2+bx+c的图象经过坐标原点,且与x轴交于A(-2,0).
如图,二次函数y=x2+bx+c的图象经过坐标原点,且与x轴交于A(-2,0).