题目内容
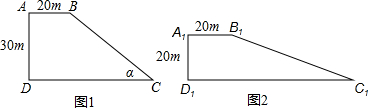
一段路基的横断面是直角梯形,如图1所示,已知原来坡面的坡角α的正弦值为0.6.
(1)求DC的长.
(2)现不改变土石方量,全部利用原有土石方进行坡面改造,使坡度变小,达到如图2所示的技术要求,试求出改造后坡面的坡角是多少?(精确到0.1度)
(1)求DC的长.
(2)现不改变土石方量,全部利用原有土石方进行坡面改造,使坡度变小,达到如图2所示的技术要求,试求出改造后坡面的坡角是多少?(精确到0.1度)

考点:解直角三角形的应用-坡度坡角问题
专题:
分析:由已知可求EC=40m.在不改变土石方量,全部充分利用原有土石方的前提下进行坡面改造,使坡度变小,则梯形ABCD面积=梯形A1B1C1D面积,可再求出EC1=80(m),即可求出改建后的坡度i=B1E:EC1=20:80=1:4.
解答: 解:(1)作BE⊥DC于E,得矩形ABED与Rt△BCE.
解:(1)作BE⊥DC于E,得矩形ABED与Rt△BCE.
在Rt△BCE中,∵sinα=
=0.6,BE=AD=30m,
∴BC=
=50m,
∴EC2=BC2-BE2=502-302=1600,
∴EC=40m,
∴DC=DE+EC=20+40=60m;
(2)作B1E1⊥D1C1于E1,在不改变土石方量,全部充分利用原有土石方的前提下进行坡面改造,使坡度变小,
则梯形ABCD面积=梯形A1B1C1D面积,
即
×(20+60)×30=
×20(20+20+E1C1),
解得E1C1=80(m),
所以改造后的坡度i=B1E1:E1C1=20:80=1:4,
∵tan14.0°=0.2493,tan14.1°=0.2511,
∴改造后坡面的坡角约为14.0°.
 解:(1)作BE⊥DC于E,得矩形ABED与Rt△BCE.
解:(1)作BE⊥DC于E,得矩形ABED与Rt△BCE.在Rt△BCE中,∵sinα=
| BE |
| BC |
∴BC=
| BE |
| sinα |
∴EC2=BC2-BE2=502-302=1600,
∴EC=40m,
∴DC=DE+EC=20+40=60m;
(2)作B1E1⊥D1C1于E1,在不改变土石方量,全部充分利用原有土石方的前提下进行坡面改造,使坡度变小,
则梯形ABCD面积=梯形A1B1C1D面积,
即
| 1 |
| 2 |
| 1 |
| 2 |
解得E1C1=80(m),
所以改造后的坡度i=B1E1:E1C1=20:80=1:4,
∵tan14.0°=0.2493,tan14.1°=0.2511,
∴改造后坡面的坡角约为14.0°.
点评:此题考查了解直角三角形的应用-坡度坡角问题,分析得出梯形ABCD面积=梯形A1B1C1D面积是解题的关键;还要熟悉坡度公式.

练习册系列答案
相关题目
下列事件中是不可能事件的是( )
| A、抛一枚硬币正面朝上 |
| B、三角形中有两个角为直角 |
| C、打开电视正在播广告 |
| D、两实数和为正 |
 如图,在△ABC中,AB=AC=10,BC=12,点E,F分别在边BC、AC上(点F不与点A、C重合)EF∥AB.把△ABC沿直线EF翻折,点C与点D重合,设FC=x.
如图,在△ABC中,AB=AC=10,BC=12,点E,F分别在边BC、AC上(点F不与点A、C重合)EF∥AB.把△ABC沿直线EF翻折,点C与点D重合,设FC=x. 如图①,△ABC中,∠ABC的外角平分线与∠ACB的外角平分线交于D.
如图①,△ABC中,∠ABC的外角平分线与∠ACB的外角平分线交于D. 四边形ABCD为正方形,点E为AB中点,点F在AD上,且AF=
四边形ABCD为正方形,点E为AB中点,点F在AD上,且AF= 把一张长方形纸片ABCD沿EF折叠,点B、C分别落在G、H的位置上,GH与CD相交于点M,EG的延长线与CD相交于点N,若∠1=55°,求∠2、∠3的度数.
把一张长方形纸片ABCD沿EF折叠,点B、C分别落在G、H的位置上,GH与CD相交于点M,EG的延长线与CD相交于点N,若∠1=55°,求∠2、∠3的度数. 如图,在平面直角坐标系中,以A(8,3)为圆心,5个单位长为半径的⊙O交x轴于点B,C两点.
如图,在平面直角坐标系中,以A(8,3)为圆心,5个单位长为半径的⊙O交x轴于点B,C两点.