题目内容
如图，圆O的半径为6，点A、B、C在圆O上，且∠ACB=45°，则弦AB的长是
- A.5
- B.6
- C.
- D.
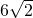
D
分析：连接OA、OB，构造圆心角∠AOB，利用圆周角定理可求∠AOB，再根据△AOB的特殊性解题．
解答：
解：连接OA、OB，
∠ACB、∠AOB为弧AB所对的圆周角和圆心角，
根据圆周角定理，得∠AOB=2∠ACB=90°，
∵OA=OB=6，
∴AB=6
．
故选D．
点评：本题考查了圆周角定理的运用，特殊直角三角形的解法．
分析：连接OA、OB，构造圆心角∠AOB，利用圆周角定理可求∠AOB，再根据△AOB的特殊性解题．
解答：
解：连接OA、OB，∠ACB、∠AOB为弧AB所对的圆周角和圆心角，
根据圆周角定理，得∠AOB=2∠ACB=90°，
∵OA=OB=6，
∴AB=6
．故选D．
点评：本题考查了圆周角定理的运用，特殊直角三角形的解法．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，圆O的半径为6，点A、B、C在圆O上，且∠ACB=45°，则弦AB的长是（ ）| A、5 | ||
| B、6 | ||
C、6
| ||
D、6
|
（2008•宝山区二模）如图，圆P的半径为2，圆心p在函数y=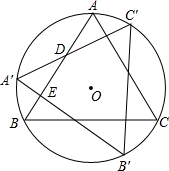
（2013•江东区模拟）如图，圆O的半径为R，正△ABC内接于圆O，将△ABC按逆时针方向旋转90°后得到△A′B′C′，它的两边与AB相交于点D、E，则以下说法正确的个数是（ ）
B．6 C．
D．5
B．6 C．
D．5