题目内容
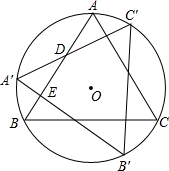（2013•江东区模拟）如图，圆O的半径为R，正△ABC内接于圆O，将△ABC按逆时针方向旋转90°后得到△A′B′C′，它的两边与AB相交于点D、E，则以下说法正确的个数是（ ）①AD=A′D；②B′E=3A′E；③tan∠ADC′=
| ||
| 3 |
| 3 |
分析：根据圆内接正三角形和旋转的性质得到∠BAC=∠B′A′C′=60°，∠C′A′O=∠OAB=30°，则∠AA'D=∠A'AD=15°，于是可得到A'D=AD；在Rt△A′DE中，根据含30度的直角三角形三边的关系得到DA′=2A′E，DE=
A′E，AE=（2+
）A′E，再利用“AAS”可证明△AA′E≌△B′BE，则AE=B′E，所以B′E=（2+
）A′E；根据30度的正切值可得到tan∠A′DB=
；在Rt△AA′E中利用勾股定理可得到AA′=
（
+1）A′E，而AA′=
R，则（
+1）A′E=R，把DE=
A′E代入得到R=（
+1）•
DE=
DE．
| 3 |
| 3 |
| 3 |
| ||
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| ||
| 3 |
3+
| ||
| 3 |
解答：解：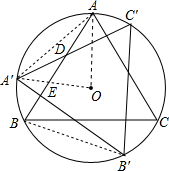
连接A'O，AO，AA′，BB′，如图，
∵△ABC是正角三角形，△ABC按逆时针方向旋转90°后得到△A′B′C′，
∴△A′B′C′为等边三角形，
∴∠BAC=∠B′A′C′=60°，
而点O为△A′B′C′的内心，
∴∠C′A′O=∠OAB=30°，
又∵∠A'OA=90°，AO=A'O，
∴△A'OA是等腰直角三角形，
∴∠AA'O=∠A'AO=45°，
∴∠AA'D=∠A'AD=15°，
∴A'D=AD，所以①正确；
∴∠A′DE=∠AA'D+∠A'AD=30°，
而∠DA′E=60°，
∴∠A′ED=90°，
∴DA′=2A′E，DE=
A′E，
∴AE=AD+DE=DA′+DE=（2+
）A′E，
∵AB=A′B′，
∴
=
，
∴
=
，
∴AA′=BB′，
在△AA′E和△B′BE中，
，
∴△AA′E≌△B′BE（AAS），
∴AE=B′E，
∴B′E=（2+
）A′E，所以②错误；
∵∠ADC'=∠A'DB=30°，
∴tan∠A′DB=tan30°=
，所以③正确；
在Rt△AA′E中，AE=（2+
）A′E，
∴AA′2=AE2+A′E2=（8+4
）A′E2，
∴AA′=
（
+1）A′E，
而AA′=
R，
∴（
+1）A′E=R，
∴R=（
+1）•
DE=
DE，所以④错误．
故选B．
连接A'O，AO，AA′，BB′，如图，∵△ABC是正角三角形，△ABC按逆时针方向旋转90°后得到△A′B′C′，
∴△A′B′C′为等边三角形，
∴∠BAC=∠B′A′C′=60°，
而点O为△A′B′C′的内心，
∴∠C′A′O=∠OAB=30°，
又∵∠A'OA=90°，AO=A'O，
∴△A'OA是等腰直角三角形，
∴∠AA'O=∠A'AO=45°，
∴∠AA'D=∠A'AD=15°，
∴A'D=AD，所以①正确；
∴∠A′DE=∠AA'D+∠A'AD=30°，
而∠DA′E=60°，
∴∠A′ED=90°，
∴DA′=2A′E，DE=
| 3 |
∴AE=AD+DE=DA′+DE=（2+
| 3 |
∵AB=A′B′，
∴
 |
| AB |
|
| A′B′ |
∴
|
| AA′ |
|
| BB′ |
∴AA′=BB′，
在△AA′E和△B′BE中，
|
∴△AA′E≌△B′BE（AAS），
∴AE=B′E，
∴B′E=（2+
| 3 |
∵∠ADC'=∠A'DB=30°，
∴tan∠A′DB=tan30°=
| ||
| 3 |
在Rt△AA′E中，AE=（2+
| 3 |
∴AA′2=AE2+A′E2=（8+4
| 3 |
∴AA′=
| 2 |
| 3 |
而AA′=
| 2 |
∴（
| 3 |
∴R=（
| 3 |
| ||
| 3 |
3+
| ||
| 3 |
故选B．
点评：本题考查了圆的综合题：熟练掌握圆周角定理和圆内接正三角形的性质；会运用勾股定理和含30度的直角三角形三边的关系进行几何运算．
练习册系列答案
开心练习课课练与单元检测系列答案
开心试卷期末冲刺100分系列答案
相关题目
（2013•江东区模拟）如图，△ABC的角平分线AD交BC于点D，点E、F分别在AB、AC上，且EF∥BC，记∠AEF=α，∠ADC=β，∠ACB的补角∠ACG为γ，则α、β、γ的关系是（ ）
（2013•江东区模拟）已知：如图，点A（-4，0），B（-1，0），将线段AB平移后得到线段CD，点A的对应点C恰好落在y轴上，且四边形ABDC的面积为9，则四边形ABDC的周长是（ ）
（2013•江东区模拟）如图，抛物线y=