题目内容
如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为1 m的圆后,在封闭图形ABCD附近闭上眼睛向封闭图形内掷小石子(可把小石子近似看成点),
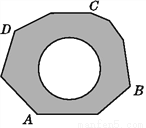
记录如下:
掷小石子所落的总次数 小石子所落的有效区域 | 50 | 150 | 300 | … |
小石子落在圆内(含圆上)的次数m | 14 | 48 | 89 | … |
小石子落在圆以外的阴影部分(含外缘)的次数n | 30 | 95 | 180 | … |
(1)当投掷的次数很大时,m∶n的值越来越接近___________(结果精确到0.1);
(2)若以小石子所落的有效区域里的次数为总数(即m+n),则随着投掷次数的增加,小石子落在圆内(含圆上)的频率稳定在___________附近;
(3)若你投一次石子,则小石子落在圆内(含圆上)的概率为___________;
(4)请你利用(2)中所得频率,估计整个封闭图形ABCD的面积是多少平方米(结果保留π).
（1）0.5；（2）；（3）；（4）3π m2
【解析】试题分析:根据表格中提供的数据计算出落在圆内的概率与落在阴影内的概率的比值,即可解答.
试题解析:(1)0.5, ≈0.5, ≈0.5, ≈0.5,所以m:n的值越来越接近0.5,
(2) 由(1)可得≈.
(3)
(4)S圆=π×12=π(m2),而≈,
所以S封闭图形ABCD≈3π m2.
如图，平行四边形ABCD中，E，F分别为边AB，DC的中点，则图中共有平行四边形的个数是 （ ）
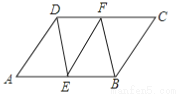
A. 3 B. 4 C. 5 D. 6
B
【解析】【解析】
∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD．
∵E，F分别AB，CD的中点，∴AE=EB=DF=FC，∴四边形AEFD是平行四边形，四边形EFCB是平行四边形，四边形BEDF是平行四边形，∴平行四边形的个数共有4个．故选B． 如图，在△ABC中，AB＝AC＝5，BC＝8，P是BC边上的动点，过点P作PD⊥AB于点D，PE⊥AC于点E，则PD+PE的长是（ ）
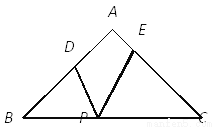
A. 4.8 B. 4.8或3.8 C. 3.8 D. 5
A
【解析】试题分析：作AF⊥BC于F，根据等腰三角形三线合一的性质得出BF=CF=4，然后根据勾股定理求得AF=3，连接AP，根据△ABC的面积=△ABP的面积+△ACP的面积解出答案即可. 分式x-y+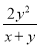
的值为（ ）
A.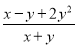 
B. x+y C. 
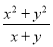D. 以上都不对
C
【解析】试题分析：原式＝
＝
＝．
故选C． 分式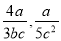
的最简公分母是_________．
15bc2
【解析】试题分析：分式与的最简公分母是15bc2．
故答案为：15bc2． 下列说法正确的是( )
A. “任意画一个三角形,其内角和为360°”是随机事件
B. 已知某篮球运动员投篮投中的概率为0.6,则他投10次可投中6次
C. 抽样调查选取样本时,所选样本可按自己的喜好选取
D. 检测某城市的空气质量,采用抽样调查法
D
【解析】试题解析：A、“任意画一个三角形，其内角和为360°”是不可能事件，故A错误；
B、已知某篮球运动员投篮投中的概率为0.6，则他投十次可能投中6次，故B错误；
C、抽样调查选取样本时，所选样本要具有广泛性、代表性，故C错误；
D、检测某城市的空气质量，采用抽样调查法，故D正确；
故选：D． 如图，BC=4cm，AB=3cm，AF=12cm，AC⊥AF，正方形CDEF的面积是169cm2，试判断△ABC的形状？
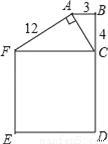
△ABC是直角三角形.
【解析】分析：首先根据正方形的面积求出FC的长，再在Rt△ACF中利用勾股定理求出AC的长，然后根据勾股定理逆定理证明∠B=90°即可．
本题解析：
∵正方形CDEF的面积是169 cm2，
∴FC=13 cm
在Rt△ACF中，由勾股定理得，
AC2=CF2﹣AF2=132﹣122=25，
在△ABC中，因为AB2+BC2=32+... 已知平行四边形ABCD中，∠B=4∠A，则∠C=__．
36°
【解析】试题解析：∵四边形BCDA是平行四边形，
∴AD∥CB，∠A=∠C，
∴∠A+∠B=180°，
∵∠B=4∠A，
∴∠A+4∠A=180°，
解得：∠A=36°，
∴∠C=36°. 如图，剪两张等宽对边平行的纸条，随意交叉叠放在一起，转动其中的一张，重合的部分构成了一个四边形，这个四边形是________．
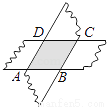
菱形
【解析】试题分析：首先可判断重叠部分为平行四边形，且两条纸条宽度相同；再由平行四边形的等积转换可得邻边相等，则四边形ABCD为菱形．所以根据菱形的性质进行判断．
【解析】
过点D分别作AB，BC边上的高为AE，AF，
∵四边形ABCD是用两张等宽的纸条交叉重叠地放在一起而组成的图形，
∴AB∥CD，AD∥BC，
∴四边形ABCD是平行四边形（对边相互平行的四边...