题目内容
8.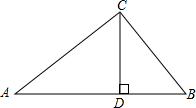 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AB=c,∠A=α,则CD长为( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AB=c,∠A=α,则CD长为( )| A. | c•sin2α | B. | c•cos2α | C. | c•sinα•tanα | D. | c•sinα•cosα |
分析 根据已知条件在Rt△ABC中,用AB和α表示BC,在Rt△DCB中,根据余弦求出CD的长,得到答案.
解答 解:在Rt△ABC中,∠ACB=90°,AB=c,∠A=α,
sinα=$\frac{BC}{AB}$,BC=c•sinα,
∠A+∠B=90°,∠DCB+∠B=90°,
∴∠DCB=∠A=α,
在Rt△DCB中,∠CDB=90°,
cos∠DCB=$\frac{CD}{BC}$,
CD=BC•cosα=c•sinα•cosα,
故选:D.
点评 本题考查的是解直角三角形的知识,掌握锐角三角函数的概念是解题的关键,把三角函数的概念看作是公式,在相应的直角三角形中,直接运用.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
18.已知圆锥的侧面积是20πcm2,母线长为5cm,则圆锥的底面半径为( )
| A. | 2cm | B. | 3cm | C. | 4cm | D. | 6cm |
20.下列各数中,无理数是( )
| A. | $\frac{22}{7}$ | B. | $\sqrt{9}$ | C. | π | D. | $\root{3}{8}$ |
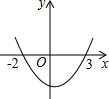 如图,抛物线y=ax2+bx+c交x轴于点A(-2,0)、B(3,0),则不等式ax2+bx+c>0的解集是x>3或x<-2.
如图,抛物线y=ax2+bx+c交x轴于点A(-2,0)、B(3,0),则不等式ax2+bx+c>0的解集是x>3或x<-2. 如图,当小明沿坡度i=1:3的坡面由A到B行走了100米,那么小明行走的水平距离AC=30$\sqrt{10}$米.(结果可以用根号表示).
如图,当小明沿坡度i=1:3的坡面由A到B行走了100米,那么小明行走的水平距离AC=30$\sqrt{10}$米.(结果可以用根号表示).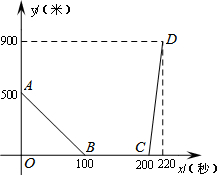 设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设x秒后两车间的距离为y千米,y关于x的函数关系如图所示,
设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设x秒后两车间的距离为y千米,y关于x的函数关系如图所示,