题目内容
3.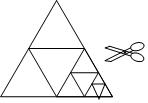 如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,第n此操作后,三角形共有(3n+1)个,若要得到100个小三角形,则需要操作的次数是33.
如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,第n此操作后,三角形共有(3n+1)个,若要得到100个小三角形,则需要操作的次数是33.
分析 由第一次操作后三角形共有4个、第二次操作后三角形共有(4+3)个、第三次操作后三角形共有(4+3+3)个,可得第n次操作后三角形共有4+3(n-1)=3n+1个,根据题意得3n+1=100,求得n的值即可.
解答 解:∵第一次操作后,三角形共有4个;
第二次操作后,三角形共有4+3=7个;
第三次操作后,三角形共有4+3+3=10个;
…
∴第n次操作后,三角形共有4+3(n-1)=(3n+1)个;
当3n+1=100时,
解得:n=33,
故答案为:3n+1,33.
点评 此题主要考查了图形的变化类问题以及三角形中位线定理的运用,根据已知得出第n次操作后,三角形的个数为3n+1是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.2017的倒数是( )
| A. | $\frac{1}{2017}$ | B. | -2017 | C. | 2017 | D. | $\sqrt{2017}$ |
15.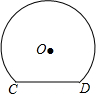 如图是一个隧道的横断面,它的形状是以点O为圆心的圆的一部分,如果圆的半径为$\frac{10}{3}$m,弦CD=4m,那么隧道的最高处到CD的距离是( )
如图是一个隧道的横断面,它的形状是以点O为圆心的圆的一部分,如果圆的半径为$\frac{10}{3}$m,弦CD=4m,那么隧道的最高处到CD的距离是( )
 如图是一个隧道的横断面,它的形状是以点O为圆心的圆的一部分,如果圆的半径为$\frac{10}{3}$m,弦CD=4m,那么隧道的最高处到CD的距离是( )
如图是一个隧道的横断面,它的形状是以点O为圆心的圆的一部分,如果圆的半径为$\frac{10}{3}$m,弦CD=4m,那么隧道的最高处到CD的距离是( )| A. | $\frac{8}{3}$m | B. | 4m | C. | $\frac{17}{3}$m | D. | 6m |
 已知:如图,第一象限内的点A,B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且tan∠ACB=$\frac{3}{2}$.
已知:如图,第一象限内的点A,B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且tan∠ACB=$\frac{3}{2}$. 如图,在圆内接四边形ABCD中,若∠A=68°,则∠C=112°.
如图,在圆内接四边形ABCD中,若∠A=68°,则∠C=112°.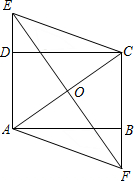 如图,在矩形ABCD中,过对角线AC的中点O作AC的垂线,分别交射线AD和CB于点E、F,连结AF、CE.
如图,在矩形ABCD中,过对角线AC的中点O作AC的垂线,分别交射线AD和CB于点E、F,连结AF、CE.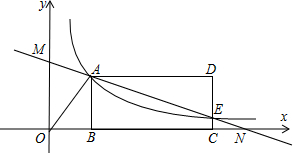 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(3,0),tan∠AOB=$\frac{4}{3}$.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(3,0),tan∠AOB=$\frac{4}{3}$.