��Ŀ����
8����ƽ��ֱ������ϵxOy�У�������y=2x2+mx+n������A��0��-2����B��3��4����1���������ߵĽ���ʽ���Գ���Ͷ��㣻
��2�����B����ԭ��ĶԳƵ�ΪC������������A��B֮��IJ���Ϊͼ��G������A��B���㣩
�ٵ�D�������߶Գ�����һ���㣬��ֱ��CD��ͼ��G�й����㣬��Ϻ���ͼ�����D������t��ȡֵ��Χ��
�ڵ�E��ͼ��G��һ���㣬����E���B����C���������������Σ�����Щ�������д���һ��������������Σ������������ε�������������ʱ��E�����꣮
���� ��1��ֱ�Ӱ�A���B���������y=2x2+mx+n��m��n�ķ����飬�ٽⷽ�������m��n���ɵõ������߽���ʽ��Ȼ��ѽ���ʽ��ɶ���ʽ���ɵõ������ߵĶԳ���Ͷ������ꣻ
��2���������ù���ԭ��ԳƵĵ�����������õ�C������Ϊ��-3��-4������ͼ��������M��1��-4������ֱ��BC��ֱ��x=1��N�㣬�ô���ϵ�������ֱ��BC�Ľ���ʽΪy=$\frac{4}{3}$x�����ڵ���D���߶�MN���˶�ʱ��ֱ��CD��ͼ��G�й����㣬���ǿɵ�t�ķ�ΧΪ-4��t��$\frac{4}{3}$���ڸ��������������ʽ����EBC����������E�㵽BC�ľ����������Eƽ����BC����������ֻ��һ��������ʱ����E��BC�ľ�����������E��ֱ�߽���ʽΪy=$\frac{4}{3}$x+b��������������ֱ�ߵĽ������⣬ͨ��������$\left\{\begin{array}{l}{y=2{x}^{2}-4x-2}\\{y=\frac{4}{3}x+b}\end{array}\right.$��һ�������b��Ψһ�⣬�Ӷ��õ�E�����꣮
��� �⣺��1����A��0��-2����B��3��4������y=2x2+mx+n��$\left\{\begin{array}{l}{n=-2}\\{18+3m+n=4}\end{array}\right.$�����$\left\{\begin{array}{l}{m=-4}\\{n=-2}\end{array}\right.$��
���������߽���ʽΪy=2x2-4x-2��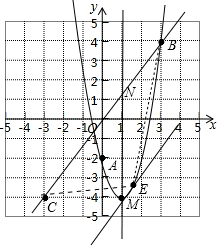
��Ϊy=2��x-1��2-4��
���������ߵĶԳ���Ϊֱ��x=1����������Ϊ��1��-4����
��2����C������Ϊ��-3��-4������ͼ������M��1��-4����ֱ��BC��ֱ��x=1��N�㣬
��ֱ��BC�Ľ���ʽΪy=kx����B��3��4�������3k=4�����k=$\frac{4}{3}$��
����ֱ��BC�Ľ���ʽΪy=$\frac{4}{3}$x��
��x=1ʱ��y=$\frac{4}{3}$����N��1��$\frac{4}{3}$����
��Ϊ����D���߶�MN���˶�ʱ��ֱ��CD��ͼ��G�й����㣬
����t�ķ�ΧΪ-4��t��$\frac{4}{3}$��
����Ϊ��EBC��������BCΪ��ֵ������E�㵽BC�ľ������
���Թ���Eƽ����BC����������ֻ��һ��������ʱ����E��BC�ľ������
�����E��ֱ�߽���ʽΪy=$\frac{4}{3}$x+b��
������$\left\{\begin{array}{l}{y=2{x}^{2}-4x-2}\\{y=\frac{4}{3}x+b}\end{array}\right.$��һ��⣬
��ȥy�õ�6x2-16x-6-3b=0����=162-4��6����-6-3b��=0�����b=-$\frac{50}{9}$��x=$\frac{4}{3}$��
��x=$\frac{4}{3}$ʱ��y=$\frac{4}{3}$��$\frac{4}{3}$-$\frac{50}{9}$=-$\frac{34}{9}$��
����E��������$\frac{4}{3}$��-$\frac{34}{9}$����
���� ���⿼���˶��κ������ۺ��⣺�������ն��κ���ͼ���ϵ�����������Ͷ��κ��������ʣ�����������ͼ�����ʣ������ô���ϵ������������ʽ����ס�����������ʽ��

 ��ְٷְټ���ϵ�д�
��ְٷְټ���ϵ�д� �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д� �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�
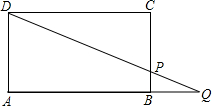 ��ͼ���ھ���ABCD�У�P��BC����һ�㣬����DP���ӳ�����AB���ӳ����ڵ�Q��
��ͼ���ھ���ABCD�У�P��BC����һ�㣬����DP���ӳ�����AB���ӳ����ڵ�Q��