题目内容
17．化简：（1）（ab-5b2+2a3）-（3ab+6a2-5b2）
（2）（a+b）-2（2a-3b）+（3a-2b）
分析 （1）先按照去括号法则去掉整式中的小括号，再合并整式中的同类项即可；
（2）先按照去括号法则去掉整式中的小括号，再合并整式中的同类项即可．
解答 解：（1）（ab-5b2+2a3）-（3ab+6a2-5b2）
=ab-5b2+2a3-3ab-6a2+5b2
=-2ab+2a3-6a2；
（2）（a+b）-2（2a-3b）+（3a-2b）
=a+b-4a+6b+3a-2b
=5b．
点评 本题考查了整式的加减、去括号法则两个考点．解决此类题目的关键是熟记去括号法则，熟练运用合并同类项的法则，这是各地中考的常考点．
练习册系列答案
相关题目
2．下列方程组中，解为$\left\{\begin{array}{l}{x=1}\\{y=1}\\{z=2}\end{array}\right.$的是（ ）
| A． | $\left\{\begin{array}{l}{x+y+z=4}\\{2x+y-z=1}\\{3x+2y-4z=-3}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x-y-z=0}\\{z+y-x=1}\\{2x+y-2x=5}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{x+y=4}\\{y+z=5}\\{x+z=6}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{2x+3y-z=5}\\{x+y+z=4}\\{x-y+2z=2}\end{array}\right.$ |
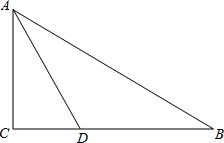已知，如图，在Rt△ABC中，∠C=90°，∠BAC的角平分线AD交BC边于D．
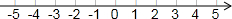在数轴上把下列各数表示出来，并用“＜”连接各数．