题目内容
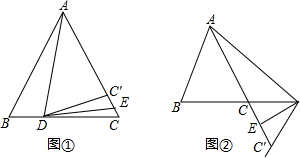
16.已知在△ABC中,AB=AC,点D是直线BC上不与点B,C重合的点,点E是射线AC上一点,为AD=AE,将∠CDE沿直线DE折叠,折叠后边DC对应的射线DC′,交射线AC于点C′.(1)如图①,当点D在BC上时,求证:AB•CC′=BD•CD;
(2)如图②,当点D在BC的延长线上时,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.
分析 (1)设∠BAD=x,根据三角形外角的性质得到∠ADC=∠B+∠BAD=∠B+x,∠AED=∠C+∠EDC,根据等腰三角形的性质得到∠B=∠C,∠ADE=∠AED,证得∠EDC=$\frac{1}{2}$∠BAD,由折叠的性质得到∠C′DC=2∠EDC,推出△ABD∽△CDC′,根据相似三角形的性质即可得到结论;
(2)根据等腰三角形的性质得到∠4=∠ADE,于是得到∠3=180°-2(∠1+∠2),由于∠B=∠ACB=∠3+∠1,于是得到180°-∠BAD-∠1=180°-2(∠1+∠2)+∠1,推出∠BAD=2∠2,得到∠CDC′=2∠2,证得△ABD∽△DCC′,根据相似三角形的性质即可得到结论.
解答 (1)证明:设∠BAD=x,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=∠B+x,
∵∠AED是△CDE的外角,
∴∠AED=∠C+∠EDC,
∵AB=AC,AD=AE,
∴∠B=∠C,∠ADE=∠AED,
∴∠ADC-∠EDC=∠B+x-∠EDC=∠B+∠EDC,
∴∠EDC=$\frac{1}{2}$∠BAD,
∵∠CDE沿直线DE折叠,折叠后边DC对应的射线DC′,
∴∠C′DC=2∠EDC,
∴∠C′DC=∠BAD,
∵∠B=∠C,
∴△ABD∽△CDC′,
∴$\frac{AB}{CD}=\frac{BD}{C′C}$,
∴AB•CC′=BD•CD;
(2)解:(1)中的结论成立,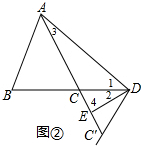
理由:∵AE=AD,
∴∠4=∠ADE,
∴∠3=180°-2(∠1+∠2),
∵AB=AC,
∴∠B=∠ACB=∠3+∠1,
∵∠B=180°-∠BAD-∠1,
∴180°-∠BAD-∠1=180°-2(∠1+∠2)+∠1,
∴∠BAD=2∠2,
∵∠ACB=∠DCC′,
∴∠B=∠DCC′,
∵将∠CDE沿直线DE折叠,折叠后边DC对应的射线DC′,
∴∠CDC′=2∠2,
∴∠BAD=∠CDC′,
∴△ABD∽△DCC′,
∴$\frac{AB}{CD}=\frac{BD}{C′C}$,
∴AB•CC′=BD•CD.
点评 本题考查了相似三角形的判定和性质,等腰三角形的性质,折叠的性质,熟练掌握相似三角形的判定和性质是解题的关键.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案| A. | $\left\{\begin{array}{l}{x+y+z=4}\\{2x+y-z=1}\\{3x+2y-4z=-3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-y-z=0}\\{z+y-x=1}\\{2x+y-2x=5}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=4}\\{y+z=5}\\{x+z=6}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x+3y-z=5}\\{x+y+z=4}\\{x-y+2z=2}\end{array}\right.$ |
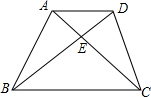 梯形ABCD中,AD∥BC,AC、BD交于E点,S△ADE:S△ADC=1:3,则S△ADE:S△DBC=$\frac{1}{4}$.
梯形ABCD中,AD∥BC,AC、BD交于E点,S△ADE:S△ADC=1:3,则S△ADE:S△DBC=$\frac{1}{4}$.
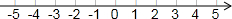 在数轴上把下列各数表示出来,并用“<”连接各数.
在数轴上把下列各数表示出来,并用“<”连接各数.