题目内容
 如图,已知矩形ABCD,把矩形沿直线AC折叠,点B落在点E处,连接DE、BE,若△ABE是等边三角形,则
如图,已知矩形ABCD,把矩形沿直线AC折叠,点B落在点E处,连接DE、BE,若△ABE是等边三角形,则| S△DCE |
| S△ABE |
考点:翻折变换(折叠问题)
专题:几何图形问题
分析:过E作EM⊥AB于M,交DC于N,根据矩形的性质得出DC=AB,DC∥AB,∠ABC=90°,设AB=AE=BE=2a,则BC=
=
a,即MN=
a,求出EN,根据三角形面积公式求出两个三角形的面积,即可得出答案.
| 2a | ||
|
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
解答:解:
过E作EM⊥AB于M,交DC于N,
∵四边形ABCD是矩形,
∴DC=AB,DC∥AB,∠ABC=90°,
∴MN=BC,EN⊥DC,
∵延AC折叠B和E重合,△AEB是等边三角形,
∴∠EAC=∠BAC=30°,
设AB=AE=BE=2a,则BC=
=
a,
即MN=
a,
∵△ABE是等边三角形,EM⊥AB,
∴AM=a,由勾股定理得:EM=
=
a,
∴△DCE的面积是
×DC×EN=
×2a×(
a-
a)=
a2,
△ABE的面积是
AB×EM=
×2a×
a=
a2,
∴
=
=
,
故答案为:
.

过E作EM⊥AB于M,交DC于N,
∵四边形ABCD是矩形,
∴DC=AB,DC∥AB,∠ABC=90°,
∴MN=BC,EN⊥DC,
∵延AC折叠B和E重合,△AEB是等边三角形,
∴∠EAC=∠BAC=30°,
设AB=AE=BE=2a,则BC=
| 2a | ||
|
| 2 |
| 3 |
| 3 |
即MN=
| 2 |
| 3 |
| 3 |
∵△ABE是等边三角形,EM⊥AB,
∴AM=a,由勾股定理得:EM=
| (2a)2-a2 |
| 3 |
∴△DCE的面积是
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| ||
| 3 |
△ABE的面积是
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴
| S△DCE |
| S△ABE |
| ||||
|
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题考查了勾股定理,折叠的性质,矩形的性质,等边三角形的性质的应用,解此题的关键是求出两个三角形的面积,题目比较典型,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
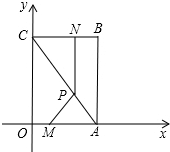 如图,在平面直角坐标系中,四边形OABC为矩形,OA=6,AB=8.动点M、N分别从O、B同时出发,都以1个单位的速度运动,其中,点M沿OA向终点C运动,点N沿BC向终点C运动,过点N作NP⊥BC,交AC于点P,连接MP,已知动点运动了x秒.
如图,在平面直角坐标系中,四边形OABC为矩形,OA=6,AB=8.动点M、N分别从O、B同时出发,都以1个单位的速度运动,其中,点M沿OA向终点C运动,点N沿BC向终点C运动,过点N作NP⊥BC,交AC于点P,连接MP,已知动点运动了x秒.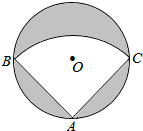 如图,有一直径是
如图,有一直径是 如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=
如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα= 如图,Rt△ABC中,∠ACB=90°,D为斜边AB的中点,AB=10cm,则CD的长为
如图,Rt△ABC中,∠ACB=90°,D为斜边AB的中点,AB=10cm,则CD的长为 如图,在平面直角坐标系中,Rt△PBD的斜边PB落在y轴上,tan∠BPD=
如图,在平面直角坐标系中,Rt△PBD的斜边PB落在y轴上,tan∠BPD= 在△ABC和△A′B′C′中,CD、C′D′平分∠ACB、∠A′C′B′,且CD=C′D′,AB=A′B′,∠ADC=∠A′D′C′,你能判断△ABC≌△A′B′C′吗?
在△ABC和△A′B′C′中,CD、C′D′平分∠ACB、∠A′C′B′,且CD=C′D′,AB=A′B′,∠ADC=∠A′D′C′,你能判断△ABC≌△A′B′C′吗?