题目内容
设a1,a2,…,a2014是从1,0,-1这三个数中取值的一列数,若a1+a2+…+a2014=69,(a1+1)2+(a2+1)2+…+(a2014+1)2=4001,则a1,a2,…,a2014中为0的个数是 .
考点:规律型:数字的变化类
专题:压轴题,规律型
分析:首先根据(a1+1)2+(a2+1)2+…+(a2014+1)2得到a12+a22+…+a20142+2152,然后设有x个1,y个-1,z个0,得到方程组
,解方程组即可确定正确的答案.
|
解答:解:(a1+1)2+(a2+1)2+…+(a2014+1)2=a12+a22+…+a20142+2(a1+a2+…+a2014)+2014
=a12+a22+…+a20142+2×69+2014
=a12+a22+…+a20142+2152,
设有x个1,y个-1,z个0
∴
,
化简得x-y=69,x+y=1849,
解得x=959,y=890,z=165
∴有959个1,890个-1,165个0,
故答案为:165.
=a12+a22+…+a20142+2×69+2014
=a12+a22+…+a20142+2152,
设有x个1,y个-1,z个0
∴
|
化简得x-y=69,x+y=1849,
解得x=959,y=890,z=165
∴有959个1,890个-1,165个0,
故答案为:165.
点评:本题考查了数字的变化类问题,解题的关键是对给出的式子进行正确的变形,难度较大.

练习册系列答案
相关题目
 在正方形ABCD中,点E为BC边的中点,点B′与点B关于AE对称,B′B与AE交于点F,连接AB′,DB′,FC.下列结论:
在正方形ABCD中,点E为BC边的中点,点B′与点B关于AE对称,B′B与AE交于点F,连接AB′,DB′,FC.下列结论:
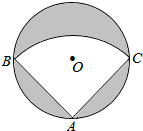 如图,有一直径是
如图,有一直径是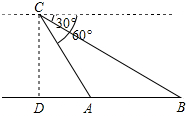 某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)
某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)