题目内容
16.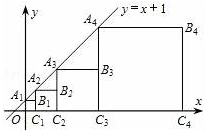 如图所示,直线y=x+1与y轴相交于点A1,以OA1为边作正方形OA1B1C1,记作第一个正方形;然后延长C1B1与直线y=x+1相交于点A2,再以C1A2为边作正方形C1A2B2C2,记作第二个正方形;同样延长C2B2与直线y=x+1相交于点A3,再以C2A3为边作正方形C2A3B3C3,记作第三个正方形;…,依此类推,则第3个正方形的边长为4,第2017个正方形的边长为22016.
如图所示,直线y=x+1与y轴相交于点A1,以OA1为边作正方形OA1B1C1,记作第一个正方形;然后延长C1B1与直线y=x+1相交于点A2,再以C1A2为边作正方形C1A2B2C2,记作第二个正方形;同样延长C2B2与直线y=x+1相交于点A3,再以C2A3为边作正方形C2A3B3C3,记作第三个正方形;…,依此类推,则第3个正方形的边长为4,第2017个正方形的边长为22016.
分析 利用一次函数图象上点的坐标特征结合正方形的性质可得出:OA1、C1A2、C2A3、C3A4、C4A5、C5A6,…,的值,根据数的变化即可得出变化规律“Cn-1An=2n-1”,依此规律即可得出结论.
解答 解:当x=0时,y=x+1=1,
∴OA1=1;
当x=1时,y=x+1=1,
∴C1A2=2;
当x=3时,y=x+1=4,
∴C2A3=4;
当x=7时,y=x+1=8,
∴C3A4=8;
同理可得出:C4A5=16,C5A6=32,…,
∴Cn-1An=2n-1.
∴C2016A2017=22016.
故答案为:4;22016.
点评 本题考查了一次函数图象上点的坐标特征以及规律型中数的变化类,根据一次函数图象上点的坐标特征结合正方形的性质找出正方形的边长的变化规律“Cn-1An=2n-1”是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.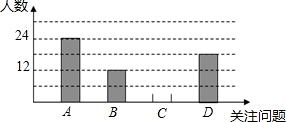 6月5日是世界环境日,中国每年都有鲜明的主题,2017世界环境日中国主题为:“绿水青山就是金山银山”,旨在释放和传递“尊重自然,顺应自然,共建美丽中国”信息,凯文同学积极学习与宣传,并从四个方面A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖,对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),以下是它收集数据后,绘制的不完整的统计图表:
6月5日是世界环境日,中国每年都有鲜明的主题,2017世界环境日中国主题为:“绿水青山就是金山银山”,旨在释放和传递“尊重自然,顺应自然,共建美丽中国”信息,凯文同学积极学习与宣传,并从四个方面A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖,对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),以下是它收集数据后,绘制的不完整的统计图表:
根据表中提供的信息解答以下问题:
(1)表中的a=60,b=0.4.
(2)请将条形统计图补充完整;
(3)如果凯文所在的学校有3600名学生,那么根据凯文提供的信息估计该校关注“全球变暖”的学生大约多少人?
 6月5日是世界环境日,中国每年都有鲜明的主题,2017世界环境日中国主题为:“绿水青山就是金山银山”,旨在释放和传递“尊重自然,顺应自然,共建美丽中国”信息,凯文同学积极学习与宣传,并从四个方面A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖,对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),以下是它收集数据后,绘制的不完整的统计图表:
6月5日是世界环境日,中国每年都有鲜明的主题,2017世界环境日中国主题为:“绿水青山就是金山银山”,旨在释放和传递“尊重自然,顺应自然,共建美丽中国”信息,凯文同学积极学习与宣传,并从四个方面A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖,对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),以下是它收集数据后,绘制的不完整的统计图表:| 关注问题 | 频数 | 频率 |
| A | 24 | b |
| B | 12 | 0.2 |
| C | n | 0.1 |
| D | 18 | m |
| 合计 | a | 1 |
(1)表中的a=60,b=0.4.
(2)请将条形统计图补充完整;
(3)如果凯文所在的学校有3600名学生,那么根据凯文提供的信息估计该校关注“全球变暖”的学生大约多少人?
7.如果M(x1,y1),N(x2,y2)是一次函数y=kx+2的图象上的两点,且x1+x2=-3,y1+y2=5,那么k的值为( )
| A. | 1 | B. | 2 | C. | -3 | D. | -$\frac{1}{3}$ |
8.已知关于x的二次函数y=-(x-h)2+3,当1≤x≤3时,函数有最小值h,则h的值为( )
| A. | -1或3 | B. | 2 | C. | 2或3 | D. | -1 |
5.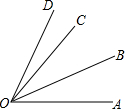 如图所示,OB是∠AOC平分线,∠COD=$\frac{1}{3}$∠BOD,∠COD=17°,则∠AOD的度数是( )
如图所示,OB是∠AOC平分线,∠COD=$\frac{1}{3}$∠BOD,∠COD=17°,则∠AOD的度数是( )
 如图所示,OB是∠AOC平分线,∠COD=$\frac{1}{3}$∠BOD,∠COD=17°,则∠AOD的度数是( )
如图所示,OB是∠AOC平分线,∠COD=$\frac{1}{3}$∠BOD,∠COD=17°,则∠AOD的度数是( )| A. | 70° | B. | 83° | C. | 68° | D. | 85° |
6. 某中学八年级的八(一)班、八(二)班分别选5名同学参加“文明创建”知识大赛活动,其预赛成绩如图所示:
某中学八年级的八(一)班、八(二)班分别选5名同学参加“文明创建”知识大赛活动,其预赛成绩如图所示:
(1)根据如图,填写下表.
(2)请从不同的角度对两班的成绩进行分析评价(至少写出三条);
(3)八(二)班选手飞飞说:“我的成绩是中等水平,”你知道他是几号选手吗?请简述理由.
 某中学八年级的八(一)班、八(二)班分别选5名同学参加“文明创建”知识大赛活动,其预赛成绩如图所示:
某中学八年级的八(一)班、八(二)班分别选5名同学参加“文明创建”知识大赛活动,其预赛成绩如图所示:(1)根据如图,填写下表.
| 平均数 | 中位数 | 众数 | 方差 | |
| 八(一)班 | 8.5 | 8.5 | 8.5 | 0.7 |
| 八(二)班 | 8.5 | 8 | 10 | 1.6 |
(3)八(二)班选手飞飞说:“我的成绩是中等水平,”你知道他是几号选手吗?请简述理由.