题目内容
9．
如图，E是?ABCD的边AD上任一点，若△EBC的面积为16，则?ABCD的面积为32．
分析 由点E是平行四边形ABCD中边AD上的任意一点，可得△EBC与?ABCD等底等高，继而可得S△EBC=$\frac{1}{2}$S?ABCD．
解答 解：∵平行四边形ABCD面积为6，
∴S△EBC=$\frac{1}{2}$S?ABCD．
∴?ABCD的面积=2×16=32；
故答案为：32．
点评 此题考查了平行四边形的性质．注意△EBC与?ABCD等底等高．
练习册系列答案
相关题目
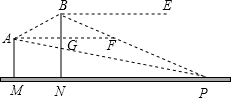某直升飞机在我方追击炮阵地M上方测得敌军雷达站P的俯角为15°，在向点P的迎面沿仰角30°的方向飞行，升高100米后再测点P的俯角为30°，分别求原飞行高度和点M到点P的水平距离（tan15°=2-$\sqrt{3}$，cot15°=2+$\sqrt{3}$）
如果将棱长相等的小正方体按如图的方式摆放，从上到下依次为第一层，第二层，第三层，…，那么第10层的小正方体的个数是55．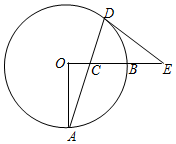
如图，OA，OB是⊙O的两条半径，OA⊥OB，C是半径OB上一动点，连结AC并延长交⊙O于D，过点D作圆的切线交OB的延长线于E，已知OA=8．
18．
如图，正方形ABCD的边长为2，连接BD，先以D为圆心，DA为半径作弧AC，再以D为圆心，DB为半径作弧BE，且D、C、E三点共线，则图中两个阴影部分的面积之和是（ ）
如图，正方形ABCD的边长为2，连接BD，先以D为圆心，DA为半径作弧AC，再以D为圆心，DB为半径作弧BE，且D、C、E三点共线，则图中两个阴影部分的面积之和是（ ）| A． | $\frac{1}{2}$π | B． | $\frac{1}{2}π$+1 | C． | π | D． | π+1 |
19．
如图，在⊙O中，AC∥OB，∠BAC=25°，则∠ADB的度数为（ ）
如图，在⊙O中，AC∥OB，∠BAC=25°，则∠ADB的度数为（ ）| A． | 55° | B． | 60° | C． | 65° | D． | 70° |