题目内容
8.已知等腰三角形一腰上的中线将这个等腰三角形的周长分成20cm和8cm两部分,求等腰三角形的底边长.分析 设腰长为xcm,底为ycm,则可知2x+y=20+8,x+$\frac{1}{2}$x=20或9,可求得y.
解答 解:设腰长为xcm,底为ycm,
则由题意可知x+$\frac{1}{2}$x=20或8,解得x=$\frac{40}{3}$或$\frac{16}{3}$,
而三角形的周长为2x+y=20+8,
当x=$\frac{40}{3}$时可解得y=8,此时三角形的三边为$\frac{40}{3}$cm,$\frac{40}{3}$cm,8cm,满足三角形的三边关系,此时底边长为8cm,
当x=$\frac{16}{3}$时可解得y=$\frac{52}{3}$,此时三角形的三边为$\frac{16}{3}$cm,$\frac{16}{3}$cm,$\frac{52}{3}$cm,不满足三角形的三边关系,不合题意;
综上可知底边长8cm.
点评 本题主要考查等腰三角形的性质,由条件分两种情况求得三角形的各边长再利用三角形的三边关系进行验证是解题的关键,注意方程思想的应用.

练习册系列答案
相关题目
16.下列说法正确的是( )
| A. | 对应边都成正比例的多边形相似 | B. | 对应角都相等的多边形相似 | ||
| C. | 等边三角形都相似 | D. | 矩形都相似 |
18.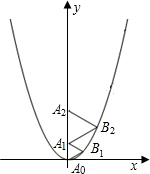 二次函数y=$\frac{2}{3}$x2的图象如图所示,点A0位于坐标原点,点 A1,A2在y轴的正半轴上,点B1,B2在二次函数y=$\frac{2}{3}$x2位于第一象限的图象上,若△A0B1A1,△A1B2A2都为等边三角形,则△A1B2A2的边长( )
二次函数y=$\frac{2}{3}$x2的图象如图所示,点A0位于坐标原点,点 A1,A2在y轴的正半轴上,点B1,B2在二次函数y=$\frac{2}{3}$x2位于第一象限的图象上,若△A0B1A1,△A1B2A2都为等边三角形,则△A1B2A2的边长( )
 二次函数y=$\frac{2}{3}$x2的图象如图所示,点A0位于坐标原点,点 A1,A2在y轴的正半轴上,点B1,B2在二次函数y=$\frac{2}{3}$x2位于第一象限的图象上,若△A0B1A1,△A1B2A2都为等边三角形,则△A1B2A2的边长( )
二次函数y=$\frac{2}{3}$x2的图象如图所示,点A0位于坐标原点,点 A1,A2在y轴的正半轴上,点B1,B2在二次函数y=$\frac{2}{3}$x2位于第一象限的图象上,若△A0B1A1,△A1B2A2都为等边三角形,则△A1B2A2的边长( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | 3 |