题目内容
13.先化简再求值:$({x+3-\frac{5}{3-x}})÷\frac{x-2}{{{x^2}-6x+9}}$,其中x是不等式2x-3(x-2)≥3的正整数解.分析 原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,求出不等式的正整数解得到x的值,代入计算即可求出值.
解答 解:原式=$\frac{(x+2)(x-2)}{x-3}$•$\frac{(x-3)^{2}}{x-2}$=(x+2)(x-3)=x2-x-6,
不等式2x-3(x-2)≥3,
去括号得:2x-3x+6≥3,
移项合并得:-x≥-3,
解得:x≤3,即正整数解为1,2,3,
当x=2与x=3时,原式没有意义,舍去;
则x=1时,原式=-6.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4. 如图,△ABC中,BD:DC=1:2,AE:EC=1:3,则S△ABO:S四边形CDOE=( )
如图,△ABC中,BD:DC=1:2,AE:EC=1:3,则S△ABO:S四边形CDOE=( )
 如图,△ABC中,BD:DC=1:2,AE:EC=1:3,则S△ABO:S四边形CDOE=( )
如图,△ABC中,BD:DC=1:2,AE:EC=1:3,则S△ABO:S四边形CDOE=( )| A. | 2:7 | B. | 2:6 | C. | 1:7 | D. | 1:6 |
18.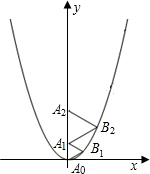 二次函数y=$\frac{2}{3}$x2的图象如图所示,点A0位于坐标原点,点 A1,A2在y轴的正半轴上,点B1,B2在二次函数y=$\frac{2}{3}$x2位于第一象限的图象上,若△A0B1A1,△A1B2A2都为等边三角形,则△A1B2A2的边长( )
二次函数y=$\frac{2}{3}$x2的图象如图所示,点A0位于坐标原点,点 A1,A2在y轴的正半轴上,点B1,B2在二次函数y=$\frac{2}{3}$x2位于第一象限的图象上,若△A0B1A1,△A1B2A2都为等边三角形,则△A1B2A2的边长( )
 二次函数y=$\frac{2}{3}$x2的图象如图所示,点A0位于坐标原点,点 A1,A2在y轴的正半轴上,点B1,B2在二次函数y=$\frac{2}{3}$x2位于第一象限的图象上,若△A0B1A1,△A1B2A2都为等边三角形,则△A1B2A2的边长( )
二次函数y=$\frac{2}{3}$x2的图象如图所示,点A0位于坐标原点,点 A1,A2在y轴的正半轴上,点B1,B2在二次函数y=$\frac{2}{3}$x2位于第一象限的图象上,若△A0B1A1,△A1B2A2都为等边三角形,则△A1B2A2的边长( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | 3 |
3.下列说法正确的是( )
| A. | -4的平方根是±2 | B. | 0的平方根与算术平方根都是0 | ||
| C. | $\sqrt{16}$的平方根是±4 | D. | (-4)2的算术平方根是-4 |
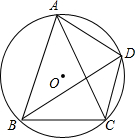 已知点A、B、C、D四点在O上;
已知点A、B、C、D四点在O上;