题目内容
已知：直线a1，a2垂直相交于O，于两直线外一点P，求作点P关于直线a1的对称点P′，点P关于直线a2的对称点P″，试证明：OP′=OP″．
考点：轴对称的性质
专题：证明题
分析：作出图形，连接PP′、PP″、OP，根据轴对称的性质可得OP′=OP，OP″=OP，然后证明即可．
解答：
证明：如图，连接PP′、PP″、OP，
∵P关于直线a1的对称点P′，
∴OP′=OP，
∵点P关于直线a2的对称点P″，
∴OP″=OP，
∴OP′=OP″．
证明：如图，连接PP′、PP″、OP，∵P关于直线a1的对称点P′，
∴OP′=OP，
∵点P关于直线a2的对称点P″，
∴OP″=OP，
∴OP′=OP″．
点评：本题考查了轴对称的性质，是基础题，熟记性质是解题的关键，作出图形更形象直观．
练习册系列答案
智能训练练测考系列答案
相关题目
有理数a、b在数轴上的位置如图所示，则下列各式不正确的是（ ）| A、a+b＜0 |
| B、ab（a-b）＞0 |
| C、-b＞0 |
| D、|b-a|=a-b |
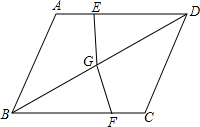如图，在四边形ABCD中，AD=BC=8，AB=CD，BD=12，点E从点D出发，以每秒1个单位的速度沿DA向点A匀速移动，点F从点C出发，以每秒3个单位的速度，沿C→B→C做匀速移动，点G从点B出发沿BD向点D匀速移动，三个点同时出发，当有一个点到达终点时，其余两点也随之停止运动，假设移动时间为t秒．