Question

15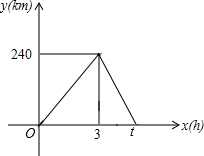．一辆轿车从甲地驶往乙地，到达乙地后返回甲地，速度是原来的1.5倍，共用t小时．设轿车行驶的时间为x（h），轿车到甲地的距离为y（km），轿车行驶过程中y与x之间的函数图象如图．
（1）求轿车从乙地返回甲地时的速度和t的值；
（2）求轿车从乙地返回甲地时y与x之间的函数关系式，并写出自变量x的取值范围．

Answer 1

分析 （1）直接利用$\frac{路程}{时间}$=速度得出轿车从甲地到乙地的速度，进而得出从乙地返回甲地的速度；
（2）利用待定系数法求出直线解析式，进而得出x的取值范围．

解答 解：（1）由函数图象知，轿车从甲地到乙地的速度为：$\frac{s}{t}$=$\frac{240}{3}$=80（km/h），
所以从乙地返回甲地的速度为1.5×80=120（km/h），
t=3+$\frac{240}{120}$=5（小时）；

（2）设轿车从乙地返回甲地时y与x之间的函数关系式为y=kx+b，
∵（3，240）和（5，0）两点在y=kx+b的函数图象上，
∴$\left\{\begin{array}{l}{5k+b=0}\\{3k+b=240}\end{array}\right.$，
解得$\left\{\begin{array}{l}{k=-120}\\{b=600}\end{array}\right.$，
∴轿车从乙地返回甲地时y与x之间的函数关系式为：y=-120x+600（3≤x≤5）．

点评 此题主要考查了一次函数的应用以及待定系数法求一次函数解析式，正确得出t的值是解题关键．