题目内容
 如图,已知AB是⊙O的直径,BC为弦,∠ABC=40°,点D为
如图,已知AB是⊙O的直径,BC为弦,∠ABC=40°,点D为 |
| BC |
考点:圆心角、弧、弦的关系
专题:
分析:先根据∠ABC=40°求出
的度数,再由AB是⊙O的直径得出
的度数,根据点D为
的中点即可得出
的度数,进而得出结论.
 |
| AC |
 |
| BC |
 |
| BC |
 |
| BD |
解答:解:∵∠ABC=40°,
∴
=80°.
∵AB是⊙O的直径,
∴
=180°-80°=100°.
∵D为
的中点,
∴
=50°,
∴∠BDC=
×50°=25°.
∴
 |
| AC |
∵AB是⊙O的直径,
∴
 |
| BC |
∵D为
 |
| BC |
∴
 |
| BD |
∴∠BDC=
| 1 |
| 2 |
点评:本题考查的是圆心角、弧、弦的关系,熟知在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一个多边形内角和是1080°,则这个多边形的对角线条数为( )
| A、26 | B、24 | C、22 | D、20 |
李红同学遇到了这样一道题:tan(α+10°)=1,你猜想锐角α的度数应是( )
| A、20° | B、35° |
| C、45° | D、50° |
 如图是轴对称图形,它的对称轴有( )
如图是轴对称图形,它的对称轴有( )| A、2条 | B、3条 | C、4条 | D、5条 |
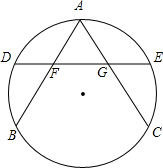 如图,A、B、C是圆O上的三点,连接
如图,A、B、C是圆O上的三点,连接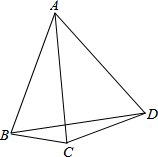 如图所示,AB=AC=AD,∠DBC=18°,则∠CAD=
如图所示,AB=AC=AD,∠DBC=18°,则∠CAD=