题目内容
7.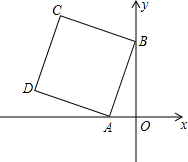 如图,A(-1,0),B(0,3),以AB为边作正方形ABCD,求C,D的坐标.
如图,A(-1,0),B(0,3),以AB为边作正方形ABCD,求C,D的坐标.
分析 证明△BCE≌△ABO,得出对应边相等BE=OA=1,CE=BO=3,同理得出DF=OA=1,AF=BO=3,再求出OE、OF,即可得出结果.
解答 解:作CE⊥y轴于E,DF⊥x轴于F,如图所示: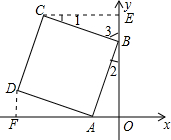 则∠CEB=∠AFD=90°,
则∠CEB=∠AFD=90°,
∴∠1+∠3=90°,
∵四边形ABCD是正方形,
∴∠ABC=90°,BC=AB,
∴∠2+∠3=90°,
∴∠1=∠2,
在△BCE和△ABO中,
$\left\{\begin{array}{l}{∠1=∠2}&{\;}\\{∠CEB=∠BOA=90°}&{\;}\\{BC=AB}&{\;}\end{array}\right.$,
∴△BCE≌△ABO(AAS),
∴BE=OA=1,CE=BO=3,
同理得:DF=OA=1,AF=BO=3,
∴OE=4,OF=4,
∴C(-3,4),D(-4,1).
点评 本题考查了正方形的性质、坐标与图形性质以及全等三角形的判定与性质;通过作辅助线证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
2.某中学为丰富学生的校园生活,准备从商店购买若干个足球和篮球,已知购买2个足球和4个篮球需420元,购买3个足球比1个篮球要多花70元.
(1)购买一个足球、一个篮球各需多少元?
(2)若学校准备用不超过1600元购买足球和篮球两种球共30个,则学校有哪几种购买方案?
(3)在”五一“期间,该商店对足球、篮球这两种商品进行如下优惠促销活动:
按上述优惠条件,七年级(1)班第一天购买足球一次性付款200元,第二天值购买篮球打折后一次性付款360元,求该班购买足球、篮球各多少个?而(2)班一次性购买这两种球,同样也是花560元,求该班购买足球、篮球各多少个?
(1)购买一个足球、一个篮球各需多少元?
(2)若学校准备用不超过1600元购买足球和篮球两种球共30个,则学校有哪几种购买方案?
(3)在”五一“期间,该商店对足球、篮球这两种商品进行如下优惠促销活动:
| 一次性购买的总金额 | 优惠措施 |
| 不超过300元 | 不优惠 |
| 超过300元且不超过500元 | 售价打九折 |
| 超过500元 | 售价打八折 |
19.|-5|的相反数是( )
| A. | -5 | B. | 5 | C. | -0.2 | D. | 0.2 |
 如图,在四边形ABCD中,∠B=40°,∠A=140°,∠C=140°,求证:四边形ABCD是平行四边形.
如图,在四边形ABCD中,∠B=40°,∠A=140°,∠C=140°,求证:四边形ABCD是平行四边形.