题目内容
20.小佳同学在学习乘法公式(a+b)2=a2±2ab+b2的多种运用后,发现可以运用所学知识上数学课时,求代数式x2+4x+5的最小值?他的解答方法如下:解:x2+4x+5=x2+4x+4+1=(x+2)2+1
∵(x+2)2≥0,
∴当x=-2时,(x+2)2的值最小,最小值是0,
∴(x+2)2+1≥1
∴当(x+2)2=0时,(x+2)2+1的值最小,最小值是1,
∴x2+4x+5的最小值是1.
请你根据上述方法,解答下列各题
(1)知识再现:当x=3时,代数式x2-6x+12的最小值是3;
(2)知识运用:若y=-x2+2x-3,当x=取何值时,y取得最大值?
分析 (1)利用配方法把原式变形,根据偶次方的非负性解答即可;
(2)利用配方法把一般式化为顶点式,根据二次函数的性质解答.
解答 解:(1)x2-6x+12=(x-3)2+3,
则x=3时,代数式的最小值是3,
故答案为:3;3;
(2)y=-x2+2x-3=-(x-1)2-2,
则当x=1时,y取得最大值是-2.
点评 本题考查的是二次函数的最值的确定,掌握配方法的一般步骤和偶次方的非负性是解题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
8.如果一个三角形的两边长分别是1cm,2cm,那么这个三角形第三边长可能是( )
| A. | 1cm | B. | 2.5cm | C. | 3cm | D. | 4cm |
8.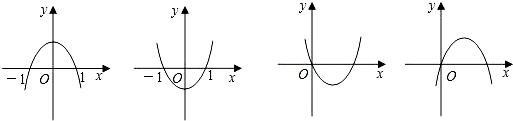 设a、b为常数,且b>0,抛物线y=ax2+bx+a2-5a-6为下列图形之一,则a的值为( )
设a、b为常数,且b>0,抛物线y=ax2+bx+a2-5a-6为下列图形之一,则a的值为( )
 设a、b为常数,且b>0,抛物线y=ax2+bx+a2-5a-6为下列图形之一,则a的值为( )
设a、b为常数,且b>0,抛物线y=ax2+bx+a2-5a-6为下列图形之一,则a的值为( )| A. | 6或-1 | B. | -6或 1 | C. | 6 | D. | -1 |
15.在Rt△ABC中,∠C=90°,a=12,b=5,则c的长为( )
| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
12.已知直线a∥b,点M到直线a的距离是5cm,到直线b的距离是3cm,那么直线a和b之间的距离是( )
| A. | 2cm | B. | 6cm | C. | 8cm | D. | 2cm或8cm |
9.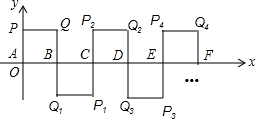 如图所示,在平面直角坐标系中A(0,0),B(1,0),P(0,1),四边形ABQP是正方形,把正方形ABQP绕点B顺时针旋转180°,得到正方形CBQ1P1;把正方形CBQ1P1绕点C顺时针旋转180°,得到正方形CDQ2P2;依此类推,则旋转第2016次后,得到的正方形的顶点P2016的坐标为( )
如图所示,在平面直角坐标系中A(0,0),B(1,0),P(0,1),四边形ABQP是正方形,把正方形ABQP绕点B顺时针旋转180°,得到正方形CBQ1P1;把正方形CBQ1P1绕点C顺时针旋转180°,得到正方形CDQ2P2;依此类推,则旋转第2016次后,得到的正方形的顶点P2016的坐标为( )
 如图所示,在平面直角坐标系中A(0,0),B(1,0),P(0,1),四边形ABQP是正方形,把正方形ABQP绕点B顺时针旋转180°,得到正方形CBQ1P1;把正方形CBQ1P1绕点C顺时针旋转180°,得到正方形CDQ2P2;依此类推,则旋转第2016次后,得到的正方形的顶点P2016的坐标为( )
如图所示,在平面直角坐标系中A(0,0),B(1,0),P(0,1),四边形ABQP是正方形,把正方形ABQP绕点B顺时针旋转180°,得到正方形CBQ1P1;把正方形CBQ1P1绕点C顺时针旋转180°,得到正方形CDQ2P2;依此类推,则旋转第2016次后,得到的正方形的顶点P2016的坐标为( )| A. | (2016,1) | B. | (2015,1) | C. | (2016,-1) | D. | (4032,1) |
10.下列问题中,两个变量成正比例关系的是( )
| A. | 弧长确定,它所对的中心角和半径 | |
| B. | 长方形的长确定,它的周长与宽 | |
| C. | 扇形的中心角确定,它的面积与半径 | |
| D. | 正多边形边数确定,它的周长与边长 |
 已知:一次越野赛中,当小明跑了1600米时,小强跑了1400米.小明,小强此后所跑的路程y(米)与时间t(秒)之间的函数关系如图所示.
已知:一次越野赛中,当小明跑了1600米时,小强跑了1400米.小明,小强此后所跑的路程y(米)与时间t(秒)之间的函数关系如图所示.