题目内容
15．在Rt△ABC中，∠C=90°，a=12，b=5，则c的长为（ ）| A． | 13 | B． | 14 | C． | 15 | D． | 16 |
分析 在Rt△ABC中，根据勾股定理求出AB即可．
解答 解：在Rt△ABC中，∠C=90°，a=12，b=5，
由勾股定理得：
c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{1{2}^{2}+{5}^{2}}$=13；
故选：A．
点评 本题考查了勾股定理；熟练掌握勾股定理，并能进行推理计算是解决问题的关键．
练习册系列答案
全能测控一本好卷系列答案
相关题目
如图，已知△ABC为等腰三角形，AB=AC，延长CB和BC至点D、点E，使得BD=CE，试说明AD=AE．
如图，将长方形ABCD沿折痕EF对折，使点C与点A重合，若∠AEB=50°，则∠AFE=65°．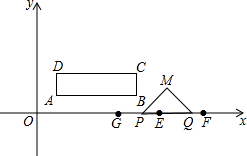
如图，矩形的四个顶点为A（1，1）、B（5，1）、C（5，2）、D（1，2），点E、F的坐标分别为（6，0）、（8，0），动点P从点E出发，以每秒2个单位长度的速度沿EO匀速运动，到达点O后立即以原来的速度沿OE返回；另一动点Q从点F出发，以每秒1个单位长度的速度沿FO匀速运动，点P、Q同时出发，两点相遇时停止运动，在点P、Q的运动过程中，以PQ为斜边在x轴上方作等腰直角三角形PQM．设运动时间为t．
10．
如图，四边形ABCD是⊙O的内接四边形，若∠B=80°，则∠ADC的度数是（ ）
如图，四边形ABCD是⊙O的内接四边形，若∠B=80°，则∠ADC的度数是（ ）| A． | 60° | B． | 80° | C． | 90° | D． | 100° |
7．
如图，在△ABC中，AB=AC，且AE=AD，∠EDC=α，则∠BAD=（ ）
如图，在△ABC中，AB=AC，且AE=AD，∠EDC=α，则∠BAD=（ ）| A． | α | B． | 2α | C． | 3α | D． | 4α |
4．
如图，已知AB，CD相交于点O，OE⊥CD于O，∠AOC=35°，则∠BOE的度数是（ ）
如图，已知AB，CD相交于点O，OE⊥CD于O，∠AOC=35°，则∠BOE的度数是（ ）| A． | 35° | B． | 55° | C． | 125° | D． | 145° |
