题目内容
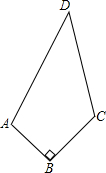 如图,四边形ABCD中,AB=6cm,BC=8cm,CD=24cm,DA=26cm,且∠ABC=90°,则四边形ABCD的面积是( )cm2.
如图,四边形ABCD中,AB=6cm,BC=8cm,CD=24cm,DA=26cm,且∠ABC=90°,则四边形ABCD的面积是( )cm2.| A、336 | B、144 |
| C、102 | D、无法确定 |
考点:勾股定理的逆定理,勾股定理
专题:
分析:利用勾股定理求出AC2的值,再由勾股定理的逆定理判定三角形ACD也为直角三角形,则S四边形ABCD=S△ABC+S△ACD.
解答:解:如图,连接AC.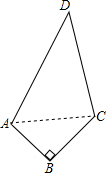
在Rt△ABC中,AC2=AB2+BC2=100,
∵AC2+CD2=AD2=676
∴△CDA也为直角三角形,
∴S四边形ABCD=S△ABC+S△ACD=
AB×BC+
AC×CD=
×6×8+
×10×24=144(cm2),
故选B.

在Rt△ABC中,AC2=AB2+BC2=100,
∵AC2+CD2=AD2=676
∴△CDA也为直角三角形,
∴S四边形ABCD=S△ABC+S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故选B.
点评:本题考查了三角形面积和勾股定理逆定理的应用,注意:在一个三角形中,如果有两边的平方和等于第三边的平方,那么这个三角形是直角三角形.

练习册系列答案
相关题目
若三角形两条边的长分别为1、5,则第三条边的长可以是( )
| A、1 | B、3 | C、5 | D、7 |
若二项式m2+1加上一个含m的单项式后是一个关于m的完全平方式,则符合要求的单项式的个数有( )
| A、4个 | B、3个 | C、2个 | D、1个 |
 如图,在?ABCD中,点E、F分别为边AD、BD上的点,EF∥AB.若DE=
如图,在?ABCD中,点E、F分别为边AD、BD上的点,EF∥AB.若DE=| 1 |
| 2 |
| A、6 | B、8 | C、12 | D、16 |
下列计算正确的是( )
| A、2x+3y=5xy |
| B、x4•x4=x16 |
| C、(4x8)÷(2x2)=2x6 |
| D、(a3)2•a4=a9 |
 如图,下列能判定AB∥CD的条件的个数是( )
如图,下列能判定AB∥CD的条件的个数是( )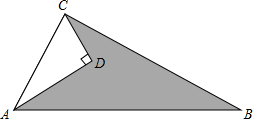 如图的一块地(图中阴影部分),∠ADC=90°,AD=12,CD=9,AB=25,BC=20.
如图的一块地(图中阴影部分),∠ADC=90°,AD=12,CD=9,AB=25,BC=20.