题目内容
 如图,在?ABCD中,点E、F分别为边AD、BD上的点,EF∥AB.若DE=
如图,在?ABCD中,点E、F分别为边AD、BD上的点,EF∥AB.若DE=| 1 |
| 2 |
| A、6 | B、8 | C、12 | D、16 |
考点:平行四边形的性质,相似三角形的判定与性质
专题:
分析:根据已知条件EF∥AB可以判定△DEF∽△DAB,则该相似三角形的对应边成比例:
=
,则易求AB=12;最后根据“平行四边形ABCD的对边相等”推知CD=AB=12.
| DE |
| DA |
| EF |
| AB |
解答: 解:如图,DE=
解:如图,DE=
EA,
∴DE=
DA.
∵EF∥AB,
∴△DEF∽△DAB,
∴
=
,即
=
,
又∵EF=4,
∴AB=12.
又∵四边形ABCD是平行四边形,
∴CD=AB=12.
故选:C.
 解:如图,DE=
解:如图,DE=| 1 |
| 2 |
∴DE=
| 1 |
| 3 |
∵EF∥AB,
∴△DEF∽△DAB,
∴
| DE |
| DA |
| EF |
| AB |
| 1 |
| 3 |
| EF |
| AB |
又∵EF=4,
∴AB=12.
又∵四边形ABCD是平行四边形,
∴CD=AB=12.
故选:C.
点评:本题考查了平行四边形的性质、相似三角形的判定与性质.此题实际上将求线段CD的长度转化为求线段AB的长度.

练习册系列答案
相关题目
下列运算,正确的是( )
| A、a+a=a2 |
| B、a•a=2a |
| C、3a3-2a2=a |
| D、2a•3a2=6a3 |
点M(x,y)的坐标满足xy>0,则点M在( )
| A、第一象限 |
| B、第一或第三象限 |
| C、第二象限 |
| D、第二或第四象限 |
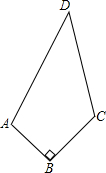 如图,四边形ABCD中,AB=6cm,BC=8cm,CD=24cm,DA=26cm,且∠ABC=90°,则四边形ABCD的面积是( )cm2.
如图,四边形ABCD中,AB=6cm,BC=8cm,CD=24cm,DA=26cm,且∠ABC=90°,则四边形ABCD的面积是( )cm2.| A、336 | B、144 |
| C、102 | D、无法确定 |
在平行四边形ABCD中,对角线AC、BD交于O点,AC=6,BD=4,则AB的取值范围是( )
| A、AB>1 |
| B、AB>2 |
| C、1<AB<5 |
| D、2<AB<10 |
下列图象中,表示直线y=x+1的是( )
A、 |
B、 |
C、 |
D、 |
 如图,已知矩形ABCD,动点E从点B沿线段BC向点C运动(点E不与B、C重合),连结AE、DE,以AE为边作矩形AG,使边FG过点D.
如图,已知矩形ABCD,动点E从点B沿线段BC向点C运动(点E不与B、C重合),连结AE、DE,以AE为边作矩形AG,使边FG过点D.