题目内容
设一元二次方程x2-6x+4=0的两个实数根分别为x1、x2，则x12+x22= ，
+
= ．
| x2 |
| x1 |
| x1 |
| x2 |
考点：根与系数的关系
专题：计算题
分析：先根据根与系数的关系得到x1+x2=6，x1x2=4，则利用完全平方公式变形得到x12+x22=（x1+x2）2-2x1x2，利用通分得到
+
=
，然后利用整体代入的方法计算．
| x2 |
| x1 |
| x1 |
| x2 |
| x12+x22 |
| x1x2 |
解答：解：根据题意得x1+x2=6，x1x2=4，
所以x12+x22=（x1+x2）2-2x1x2=62-2×4=28，
+
=
=
=7．
故答案为28，7．
所以x12+x22=（x1+x2）2-2x1x2=62-2×4=28，
| x2 |
| x1 |
| x1 |
| x2 |
| x12+x22 |
| x1x2 |
| 28 |
| 4 |
故答案为28，7．
点评：本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-
，x1x2=
．
| b |
| a |
| c |
| a |
练习册系列答案
相关题目
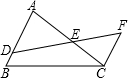如图，在△ABC中，D是AB上的一点，DF交AC于点E，有下列3个论断：①DE=EF；