题目内容
19. 如图,已知矩形ABCD,一条直线把矩形分割成两个多边形,若两个多边形的内角和分别为M和N,则M+N的最小值为360°.
如图,已知矩形ABCD,一条直线把矩形分割成两个多边形,若两个多边形的内角和分别为M和N,则M+N的最小值为360°.
分析 根据多边形内角和定理:(n-2)•180°,列出M+N的式子,然后求出最小值.
解答 解:一条直线将该矩形ABCD分割成两个多边形,
设两个多边形的分别为m边形和n边形,
则M+N=(m-2)×180°+(n-2)×180°,
∵m≥3,n≥3,
∴M+N≥360°,
即最小值为:360°.
故答案为:360°.
点评 此题主要考查了多边形的内角与外角,解答本题的关键是掌握多边形的内角和定理,题目比较简单.

练习册系列答案
相关题目
14.已知点P(a-1,a+2)在平面直角坐标系的第二象限内,则a的取值范围为( )
| A. | a<1 | B. | -2<a<1 | C. | a<-2 | D. | -2≤a≤1 |
4.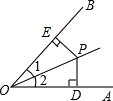 如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,下列结论错误的是( )
如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,下列结论错误的是( )
 如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,下列结论错误的是( )
如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,下列结论错误的是( )| A. | PD=PE | B. | OD=OE | C. | ∠DPO=∠EPO | D. | PD=OD |
9.下列直线表示的不是y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
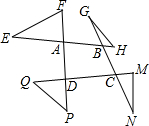 如图,以四边形ABCD各顶点及各边延长线上的点构成△AEF、△BGH、△CMN、△DPQ,求∠E+∠F+∠G+∠H+∠M+∠N+∠P+∠Q的度数.
如图,以四边形ABCD各顶点及各边延长线上的点构成△AEF、△BGH、△CMN、△DPQ,求∠E+∠F+∠G+∠H+∠M+∠N+∠P+∠Q的度数.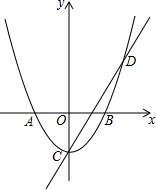 如图,在平面直角坐标系中,抛物线与x轴交于点A(-1,0)和点B(1,0),直线y=2x-1与y轴交于点C,与抛物线交于点C、D.
如图,在平面直角坐标系中,抛物线与x轴交于点A(-1,0)和点B(1,0),直线y=2x-1与y轴交于点C,与抛物线交于点C、D. 从而可得该不等式组的解集为1≤x<4.
从而可得该不等式组的解集为1≤x<4.