Question

4．在Rt△ABC中，∠C=90°，AC=6，BC=8，如图甲，⊙O是Rt△ABC的内切圆，则有⊙O的半径r=2；如图乙若半径r_n的n个等圆⊙O₁、⊙O₂…⊙O_n依次外切，且⊙O₁与AC、AB相切，⊙O₁、⊙O₂…⊙O_n均与AB相切，则r_n的值为$\frac{10}{2n+3}$．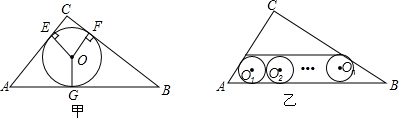

Answer 1

分析 如图，作辅助线；首先求出O₁O_n、CH、CK的长度；运用${S}_{△ABC}={S}_{△A{O}_{1}C}+{S}_{△B{O}_{n}C}$${S}_{△C{O}_{1}{O}_{n}}+{S}_{梯形A{O}_{1}{O}_{n}B}$，列出关于r_n的等式，求出r_n即可解决问题．

解答 解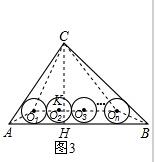：如图，连接AO₁，BO_n，CO₁，CO_n，O₁O_n，则
${S}_{△A{O}_{1}C}$=$\frac{1}{2}$AC•r_n=3r_n，${S}_{△B{O}_{n}C}$=$\frac{1}{2}$BC•r_n=4r_n，
∵等圆⊙O₁，⊙O₂，…⊙O_n依次外切，且均与AB边相切，
∴O₁，O₂，…，O_n均在直线O₁O_n上，且O₁O_n∥AB，
∴O₁O_n=（n-2）2r_n+2r_n=2（n-1）r_n，
过点C作CH⊥AB于点H，交O₁O_n于点K，
则CH=$\frac{24}{5}$，CK=$\frac{24}{5}-{r}_{n}$；
${S}_{△C{O}_{1}{O}_{n}}=\frac{1}{2}{O}_{1}{O}_{n}•CK$=（n-1）（$\frac{24}{5}$-r_n）r_n，
${S}_{梯形A{O}_{1}{O}_{n}B}=\frac{1}{2}[2（n-1）{r}_{n}+10]{r}_{n}$=[（n-1）r_n+5]r_n；
∵${S}_{△ABC}={S}_{△A{O}_{1}C}+{S}_{△B{O}_{n}C}$+${S}_{△C{O}_{1}{O}_{n}}+{S}_{梯形A{O}_{1}{O}_{n}B}$，
∴24=$3{r}_{n}+4{r}_{n}+（n-1）（\frac{24}{5}-{r}_{n}）{r}_{n}$+[（n-1）r_n+5]r_n，
解得：${r}_{n}=\frac{10}{2n+3}$

点评 该题以相切两圆为基础，以相切两圆的性质为考查的核心构造而成；解题的关键是作辅助线，灵活运用三角形内切圆的性质、三角形的面积公式等来表示图形中面积之间的等量关系．