题目内容
20.在△ABC中,∠A=30°,D是AC边上的点;先将△ABC沿着BD翻折,翻折后△ABD的边AB交AC于点E;又将△BCE沿着BE翻折,C点恰好落在BD上,此时∠BEC=78°,则原三角形的∠ABC=72度.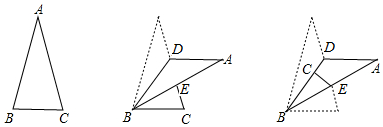
分析 在图①的△ABC中,根据三角形内角和定理,可求得∠B+∠C=150°;结合折叠的性质和图②③可知:∠B=3∠CBD,即可在△CBD中,得到另一个关于∠B、∠C度数的等量关系式,联立两式即可求得∠B的度数.
解答 解:在△ABC中,∠A=30°,则∠B+∠C=150°…①;
根据折叠的性质知:∠B=3∠CBE,∠BCE=∠C;
在△CBE中,则有:∠CBE+∠BCE=180°-78°,即:
| 1 |
| 3 |
①-②,得:
| 2 |
| 3 |
解得∠B=72°.
故答案为:72.
点评 此题主要考查的是图形的折叠变换及三角形内角和定理的应用,能够根据折叠的性质发现∠B和∠CBD的倍数关系是解答此题的关键.

练习册系列答案
相关题目
8.有下列四个数:$\sqrt{9}$,-$\frac{1}{3}$,0.080080008,$\sqrt{5}$,其中无理数是( )
| A. | $\sqrt{9}$ | B. | -$\frac{1}{3}$ | C. | 0.080080008 | D. | $\sqrt{5}$ |
15.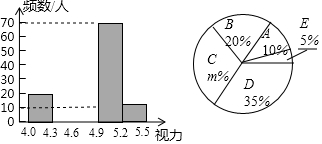 某市对参加2016年中考的4000名初中毕业生进行了一次视力抽样调查,并根据统计数据,制作了如图所示的统计表和统计图.
某市对参加2016年中考的4000名初中毕业生进行了一次视力抽样调查,并根据统计数据,制作了如图所示的统计表和统计图.
请根据图表信息回答下列问题:
(1)求抽样调查的人数;
(2)a=40,b=60,m=30;
(3)补全频数分布直方图;
(4)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是40%;根据上述信息估计该市2016年中考的初中毕业生视力正常的学生大约有多少人.
 某市对参加2016年中考的4000名初中毕业生进行了一次视力抽样调查,并根据统计数据,制作了如图所示的统计表和统计图.
某市对参加2016年中考的4000名初中毕业生进行了一次视力抽样调查,并根据统计数据,制作了如图所示的统计表和统计图.| 组别 | 视力 | 频数(人) |
| A | 4.0≤x<4.3 | 20 |
| B | 4.3≤x<4.6 | a |
| C | 4.6≤x<4.9 | b |
| D | 4.9≤x<5.2 | 70 |
| E | 5.2≤x<5.5 | 10 |
(1)求抽样调查的人数;
(2)a=40,b=60,m=30;
(3)补全频数分布直方图;
(4)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是40%;根据上述信息估计该市2016年中考的初中毕业生视力正常的学生大约有多少人.
12.下列四个点,在正比例函数y=$\frac{2}{5}$x的图象上的点是( )
| A. | (2,5) | B. | (5,2) | C. | (2,-5) | D. | (5,-2) |
 如图,AB∥CD∥EF,写出∠B、∠D、∠BED之间的数量关系,并说明理由.
如图,AB∥CD∥EF,写出∠B、∠D、∠BED之间的数量关系,并说明理由.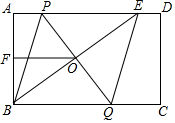 如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.