题目内容
18. 在如图所示网格内建立恰当直角坐标系后,画出函数y=x2和y=-$\frac{1}{2}$x2的图象,并根据图象回答下列问题(设小方格的边长为1):
在如图所示网格内建立恰当直角坐标系后,画出函数y=x2和y=-$\frac{1}{2}$x2的图象,并根据图象回答下列问题(设小方格的边长为1):(1)抛物线y=x2,当x≠0时,抛物线上的点都在x轴的上方,它的顶点是图象的最低点;
(2)函数y=-$\frac{1}{2}$x2,对于一切x的值,总有函数y≤0;当x=0时,y有最大值是0.
分析 根据二次函数的性质,由开口方向、对称轴、顶点坐标作出函数图象.
(1)根据画出的函数图象并结合其性质即可求解;
(2)结合函数图象,根据二次函数的性质即可求解.
解答 解;画出函数y=x2和y=-$\frac{1}{2}$x2的图象如图: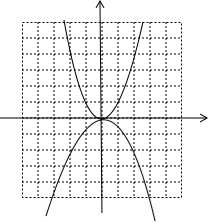
(1)抛物线y=x2,当x≠0时,抛物线上的点都在x轴的上方,它的顶点是图象的最低点;
(2)函数y=-$\frac{1}{2}$x2,对于一切x的值,总有函数y≤0,当x=0时,y有最大值是0.
故答案为≠0,低,≤,=0,大,0.
点评 本题结合图象考查了二次函数的性质,重点是注意函数的开口方向、顶点坐标、对称轴及单调性与最值的问题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 作图:以直线MN为对称轴,画出△DEF,使它与△ABC关于直线MN成轴对称.
作图:以直线MN为对称轴,画出△DEF,使它与△ABC关于直线MN成轴对称.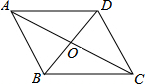 如图,AB∥CD,AD∥BC,AC与BD交于点O,那么图中全等的三角形共有4对.
如图,AB∥CD,AD∥BC,AC与BD交于点O,那么图中全等的三角形共有4对.