题目内容
已知关于x的一元二次方程:mx2-(4m+1)x+3m+3=0.
(1)求证:方程总有两个实根;
(2)若m是整数,方程的根也是整数,求m的值.
(1)求证:方程总有两个实根;
(2)若m是整数,方程的根也是整数,求m的值.
考点:根的判别式
专题:
分析:(1)根据题意m≠0,则计算判别式有△=(2m-1)2≥0,然后根据判别式的意义即可得到结果;
(2)利用求根公式得到x1=3,x2=1+
,而方程的两个实数根都是整数,且m为整数,然后根据整数的整除性即可得到m的值.
(2)利用求根公式得到x1=3,x2=1+
| 1 |
| m |
解答:(1)证明:∵方程mx2-(4m+1)x+3m+3=0是关于x的一元二次方程,
∴m≠0,
∵△=(4m+1)2-4m×(3m+3)=(2m-1)2≥0,
∴此方程总有两个实数根;
(2)解:方程的两个实数根为x=
,
∴x1=3,x2=1+
,
∵m是整数,方程的根也是整数,
∴m=±1.
∴m≠0,
∵△=(4m+1)2-4m×(3m+3)=(2m-1)2≥0,
∴此方程总有两个实数根;
(2)解:方程的两个实数根为x=
| 4m+1±(2m-1) |
| 2m |
∴x1=3,x2=1+
| 1 |
| m |
∵m是整数,方程的根也是整数,
∴m=±1.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的解.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
下列等式变形正确的是( )
| A、如果ax=bx,那么a=b | ||||
| B、如果2x+7=2y+7,那么x=y | ||||
C、如果4x=8,那么x=
| ||||
D、如果S=
|
如图是甲乙两个学校男女人数统计图,女生人数多的学校是( )


| A、甲校 | B、乙校 |
| C、两个学校人数一样多 | D、无法确定 |
 如图,在Rt△ABC中,∠C=90°,∠B=15°,DE垂直平分AB交BC于点E,BE=4,则AC长为( )
如图,在Rt△ABC中,∠C=90°,∠B=15°,DE垂直平分AB交BC于点E,BE=4,则AC长为( )| A、2 | B、3 |
| C、4 | D、2,3,4以外的值 |
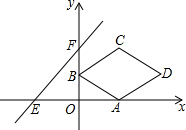 如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),点C在第一象限,对角线BD与x轴平行.直线y=x+3与x轴、y轴分别交于点E,F.将菱形ABCD沿x轴向左平移m个单位,当点D落在△EOF的内部时(不包括三角形的边),m的值可能是( )
如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),点C在第一象限,对角线BD与x轴平行.直线y=x+3与x轴、y轴分别交于点E,F.将菱形ABCD沿x轴向左平移m个单位,当点D落在△EOF的内部时(不包括三角形的边),m的值可能是( ) 如图,在四边形ABCD中,AB=AD=2,∠A=60°,BC=2
如图,在四边形ABCD中,AB=AD=2,∠A=60°,BC=2
 如图,直线y=-x+5分别与x轴、y轴交于A、B两点.
如图,直线y=-x+5分别与x轴、y轴交于A、B两点.