题目内容
9.已知y1=$\frac{1}{3}$(x+2),y2=$\frac{1}{2}$x-1,如果y1=3y2-1,求x的值.分析 由y1=$\frac{1}{3}$(x+2),y2=$\frac{1}{2}$x-1,可得等式$\frac{1}{3}$(x+2)=3($\frac{1}{2}$x-1)-1,解方程即可求得x的值.
解答 解:∵y1=3y2-1,
∴$\frac{1}{3}$(x+2)=3($\frac{1}{2}$x-1)-1,
$\frac{1}{3}$x+$\frac{2}{3}$=$\frac{3}{2}$x-3-1,
移项得:$\frac{1}{3}$x-$\frac{3}{2}$x>-4-$\frac{2}{3}$,
即-$\frac{7}{6}$x>-$\frac{14}{3}$,
系数化1得:x=4.
点评 本题考查了解一元一次方程的应用,解答此题的关键是由题意列出等式解此方程即可.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
19.|-4|的算术平方根是( )
| A. | 16 | B. | 4 | C. | ±2 | D. | 2 |
20.化简(a-b)2•(b-a)3的结果是( )
| A. | (a-b)5 | B. | (b-a)5 | C. | (a-b)6 | D. | b6-a6 |
 如图,点G是Rt△ABC的重心,过点G作矩形GECF,当GF:GE=1:2时,则∠A的正切值.
如图,点G是Rt△ABC的重心,过点G作矩形GECF,当GF:GE=1:2时,则∠A的正切值.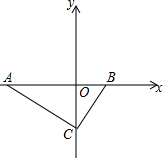 如图,在平面直角坐标系中,点A在x轴的负半轴上,点B在x轴的正半轴上.C在y轴的负半轴上,AC所在直线为y=kx-12.AC⊥BC.BC的长的$\frac{1}{3}$倍是方程x2-3x-10=0的根.
如图,在平面直角坐标系中,点A在x轴的负半轴上,点B在x轴的正半轴上.C在y轴的负半轴上,AC所在直线为y=kx-12.AC⊥BC.BC的长的$\frac{1}{3}$倍是方程x2-3x-10=0的根.