题目内容
9.求证:$\sqrt{{a}^{2}+\frac{1}{{b}^{2}}+\frac{{a}^{2}}{(ab+1)^{2}}}$=|a+$\frac{1}{b}$-$\frac{1}{ab+1}$|.分析 根据完全平分公式,再利用二次根式的性质,进行解答即可.
解答 解:∵$(a+\frac{1}{b}-\frac{1}{ab+1})^{2}$
=${a}^{2}+\frac{1}{{b}^{2}}+\frac{1}{(ab+1)^{2}}$+2[$\frac{a}{b}-\frac{{a}^{2}}{ab+1}-\frac{a}{b(ab+1)}$]
=${a}^{2}+\frac{1}{{b}^{2}}+\frac{1}{(ab+1)^{2}}$+2[$\frac{a(ab+1)-{a}^{2}b-{a}^{\;}}{b(ab+1)}$]
=${a}^{2}+\frac{1}{{b}^{2}}+\frac{1}{(ab+1)^{2}}$
∴$\sqrt{{a}^{2}+\frac{1}{{b}^{2}}+\frac{{a}^{2}}{(ab+1)^{2}}}$=|a+$\frac{1}{b}$-$\frac{1}{ab+1}$|.
点评 本题考查了二次根式的性质与化简,解决本题的关键是利用完全平分公式进行证明.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
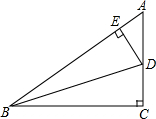 在Rt△ABC中,BD平分∠ABC,DE⊥AB于E,若AB=10,BC=8,AC=6,求△AED的周长.
在Rt△ABC中,BD平分∠ABC,DE⊥AB于E,若AB=10,BC=8,AC=6,求△AED的周长.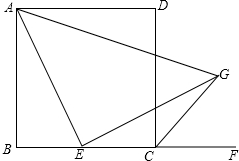 如图,E为正方形ABCD的边BC上一点,CG平分∠DCF,连接AE,过点E作EG⊥AE交CG于点G.求证:AE=EG.
如图,E为正方形ABCD的边BC上一点,CG平分∠DCF,连接AE,过点E作EG⊥AE交CG于点G.求证:AE=EG.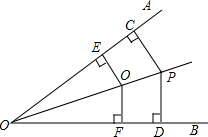 如图,PC⊥OA于点C,PD⊥OB于点D,PC=PD,Q是OP上一点,QE⊥OA于点E,QF⊥OB于点F,求证:QE=QF.
如图,PC⊥OA于点C,PD⊥OB于点D,PC=PD,Q是OP上一点,QE⊥OA于点E,QF⊥OB于点F,求证:QE=QF.